library(tidyverse)
library(palmerpenguins)
library(nycflights13)2.1 Pré-requis
Nous avons ici besoin des packages suivants :
Pensez à les charger en mémoire si ce n’est pas déjà fait ou si vous venez de démarrer une nouvelle session de travail.
2.2 La notion de dispersion
Comme expliqué plus haut, les indices de dispersion nous renseignent sur la variabilités des données autour de la valeur centrale (moyenne ou médiane) d’une population ou d’un échantillon. L’écart-type, la variance et l’intervalle interquartile sont 3 exemples d’indices de dispersion. Prenons l’exemple de l’écart-type. Un écart-type faible indique que la majorité des observations ont des valeurs proches de la moyenne. À l’inverse, un écart-type important indique que la plupart des points sont éloignés de la moyenne. L’écart-type est une caractéristique de la population que l’on étudie grâce à un échantillon, au même titre que la moyenne. En travaillant sur un échantillon, on espère accéder aux vraies grandeurs de la population. Même si ces vraies grandeurs sont à jamais inaccessibles (on ne connaîtra jamais parfaitement quelle est la vraie valeur de moyenne \(\mu\) ou d’écart-type \(\sigma\) de la population), on espère qu’avec un échantillonnage réalisé correctement, la moyenne de l’échantillon (\(\bar{x}\) ou \(m\)) et l’écart-type (\(s\)) de l’échantillon reflètent assez fidèlement les valeurs de la population générale. C’est la notion d’estimateur, intimement liée à la notion d’inférence statistique : la moyenne de l’échantillon, que l’on connait avec précision, est un estimateur de la moyenne \(\mu\) de la population qui restera à jamais inconnue. C’est la raison pour laquelle la moyenne de l’échantillon est parfois notée \(\hat{\mu}\) (en plus de \(\bar{x}\) ou \(m\)). De même, l’écart-type \(s\) et la variance \(s^2\) d’un échantillon sont des estimateurs de l’écart-type \(\sigma\) et de la variance \(\sigma^2\) de la population générale. C’est la raison pour laquelle on les note parfois \(\hat{\sigma}\) et \(\hat{\sigma}^2\) respectivement. L’accent circonflexe se prononce “chapeau”. On dit donc que \(\hat{\sigma}\) (sigma chapeau, l’écart-type de l’échantillon) est un estimateur de l´écart-type de la population générale. Comme nous l’avons vu, les indices de dispersion doivent accompagner les indices de position lorsque l’on décrit des données, car présenter une valeur de moyenne, ou de médiane seule n’a pas de sens : il faut savoir à quel point les données sont proches ou éloignées de la tendance centrale pour savoir si, dans la population générale, les indicateurs de position correspondent ou non, aux valeurs portées par la majorité des individus.
Nous avons vu plus haut comment calculer des indices de position et de dispersion. Tout ceci devrait donc être clair pour vous à ce stade.
2.3 La notion d’incertitude
Par ailleurs, puisqu’on ne sait jamais avec certitude si nos estimations (de moyennes ou d’écarts-types ou de tout autre paramètre) reflètent fidèlement ou non les vraies valeurs de la population, nous devons quantifier à quel point nos estimations s’écartent de celles de la population générale. C’est tout l’intérêt des statistiques et c’est ce que permettent les indices d’incertitude : on ne connaîtra jamais la vraie valeur de moyenne ou d’écart-type de la population, mais on peut quantifier à quel point nos estimations (basées sur un échantillon) sont précises ou imprécises.
Les deux indices d’incertitude les plus connus (et les plus utilisés) sont l’intervalle de confiance à 95% (de la moyenne ou de tout autre estimateur ; les formules sont nombreuses et il n’est pas utile de les détailler ici : nous verrons comment les calculer plus bas) et l’erreur standard de la moyenne (\(se_{\bar{x}}\)), dont la formule est la suivante :
\[se_{\bar{x}} = \frac{s}{\sqrt{n}}\] avec \(s\), l’écart-type de l’échantillon et \(n\) la taille de l’échantillon.
Comme pour la moyenne, on peut calculer l’erreur standard d’un écart-type, d’une médiane, d’une proportion, ou de tout autre estimateur calculé sur un échantillon. Cet indice d’incertitude ne nous renseigne pas sur une grandeur de la population générale qu’on chercherait à estimer, mais bien sur l’incertitude associée à une estimation que nous faisons en travaillant sur un échantillon de taille forcément limitée. Tout processus d’échantillonnage est forcément entaché d’incertitude, causée entre autre par le hasard de l’échantillonnage (ou fluctuation d’échantillonnage). Puisque nous travaillons sur des échantillons forcément imparfaits, les indices d’incertitude vont nous permettre de quantifier à quel point nos estimations s’écartent des vraies valeurs de la population. Ces “vraies valeurs”, faute de pouvoir collecter tous les individus de la population, resteront à jamais inconnues.
Quand on étudie des populations naturelles grâce à des échantillons on se trompe toujours. Les statistiques nous permettent de quantifier à quel point on se trompe grâce aux indices d’incertitude, et c’est déjà pas mal !
En examinant la formule de l’erreur standard de la moyenne présentée ci-dessus, on comprend intuitivement que plus la taille de l’échantillon (\(n\)) augmente, plus l’erreur standard (donc l’incertitude) associée à notre estimation de moyenne diminue. Autrement dit, plus les données sont abondantes dans l’échantillon, meilleure sera notre estimation de moyenne, et donc, moins le risque de raconter des bêtises sera grand.
L’autre indice d’incertitude très fréquemment utilisé est l’intervalle de confiance à 95% (de la moyenne, de la médiane, de la variance, ou de toute autre estimateur calculé dans un échantillon). L’intervalle de confiance nous renseigne sur la gamme des valeurs les plus probables pour un paramètre de la population étudiée. Par exemple, si j’observe, dans un échantillon, une moyenne de 10, avec un intervalle de confiance calculé de [7 ; 15], cela signifie que, dans la population générale, la vraie valeur de moyenne a de bonnes chances de se trouver dans l’intervalle [7 ; 15]. Dans la population générale, toutes les valeurs comprises entre 7 et 15 sont vraisemblables pour la moyenne alors que les valeurs situées en dehors de cet intervalle sont moins probables. Une autre façon de comprendre l’intervalle de confiance est de dire que si je récupère un grand nombre d’échantillons dans la même population, en utilisant exactement le même protocole expérimental, 95% des échantillons que je vais récupérer auront une moyenne située à l’intérieur de l’intervalle de confiance à 95%, et 5% des échantillons auront une moyenne située à l’extérieur de l’intervalle de confiance à 95%. C’est une notion qui n’est pas si évidente que ça à comprendre, donc prenez bien le temps de relire cette section si besoin, et de poser des questions le cas échéant.
Concrètement, plus l’intervalle de confiance est large, moins notre confiance est grande. Si la moyenne d’un échantillon vaut \(\bar{x} = 10\), et que son intervalle de confiance à 95% vaut [9,5 ; 11], la gamme des valeurs probables pour la moyenne de la population est étroite. Autrement dit, la moyenne de l’échantillon (10), a de bonne chances d’être très proche de la vraie valeur de moyenne de la population générale (vraisemblablement comprise quelque part entre 9,5 et 11). À l’inverse, si l’intervalle de confiance à 95% de la moyenne vaut [4 ; 17], la gamme des valeurs possibles pour la vraie moyenne de la population est grande. La moyenne de l’échantillon aura donc de grandes chances d’être assez éloignée de la vraie valeur de la population.
La notion d’intervalle de confiance à 95% est donc très proche de celle d’erreur standard. D’ailleurs, pour de nombreux paramètres, l’intervalle de confiance est calculé à partir de l’erreur standard.
2.4 Calcul de l’erreur standard de la moyenne
Contrairement aux indices de position et de dispersion, il n’existe pas de fonction intégrée à R qui permette de calculer l’erreur standard de la moyenne. Toutefois, sa formule très simple nous permet de la calculer à la main quand on en a besoin grâce à la fonction summarise().
Par exemple, reprenons les données de température (tableau weather du package nycflights13, colonne temp) dans les 3 aéroports de New York (colonne origin). Imaginons que nous souhaitions étudier les fluctuations de températures au fil des mois de l’année 2013 :
- Je vais commencer par transformer les températures (fournies en degrés Fahrenheit) en degrés Celsius :
weather |>
mutate(temp_celsius = (temp - 32) / 1.8)# A tibble: 26,115 × 16
origin year month day hour temp dewp humid wind_dir wind_speed
<chr> <int> <int> <int> <int> <dbl> <dbl> <dbl> <dbl> <dbl>
1 EWR 2013 1 1 1 39.0 26.1 59.4 270 10.4
2 EWR 2013 1 1 2 39.0 27.0 61.6 250 8.06
3 EWR 2013 1 1 3 39.0 28.0 64.4 240 11.5
4 EWR 2013 1 1 4 39.9 28.0 62.2 250 12.7
5 EWR 2013 1 1 5 39.0 28.0 64.4 260 12.7
6 EWR 2013 1 1 6 37.9 28.0 67.2 240 11.5
7 EWR 2013 1 1 7 39.0 28.0 64.4 240 15.0
8 EWR 2013 1 1 8 39.9 28.0 62.2 250 10.4
9 EWR 2013 1 1 9 39.9 28.0 62.2 260 15.0
10 EWR 2013 1 1 10 41 28.0 59.6 260 13.8
# ℹ 26,105 more rows
# ℹ 6 more variables: wind_gust <dbl>, precip <dbl>, pressure <dbl>,
# visib <dbl>, time_hour <dttm>, temp_celsius <dbl>- Ensuite, je détermine, pour chaque jour de chaque mois de l’année, et pour chaque aéroport, quelle est la température maximale atteinte, et je stocke ces valeurs dans un nouvel objet pour pouvoir le ré-utiliser :
temp_jour <- weather |>
mutate(temp_celsius = (temp - 32) / 1.8) |>
summarise(temperature_max = max(temp_celsius, na.rm = TRUE),
.by = c(origin, month, day))
temp_jour# A tibble: 1,092 × 4
origin month day temperature_max
<chr> <int> <int> <dbl>
1 EWR 1 1 5
2 EWR 1 2 1.10
3 EWR 1 3 1.10
4 EWR 1 4 4.4
5 EWR 1 5 6.7
6 EWR 1 6 8.9
7 EWR 1 7 8.3
8 EWR 1 8 9.4
9 EWR 1 9 10
10 EWR 1 10 10
# ℹ 1,082 more rows- Je peux maintenant calculer la température moyenne mensuelle pour chaque aéroport :
temp_jour |>
summarise(moyenne = mean(temperature_max, na.rm = TRUE),
.by = c(origin, month))# A tibble: 36 × 3
origin month moyenne
<chr> <int> <dbl>
1 EWR 1 5.69
2 EWR 2 4.74
3 EWR 3 8.20
4 EWR 4 16.4
5 EWR 5 22.2
6 EWR 6 27.4
7 EWR 7 31.0
8 EWR 8 27.8
9 EWR 9 24.6
10 EWR 10 20.0
# ℹ 26 more rowsPour pouvoir réutiliser ce tableau, je lui donne un nom :
temp_moyennes <- temp_jour |>
summarise(moyenne = mean(temperature_max, na.rm = TRUE),
.by = c(origin, month))Au final, je peux faire un graphique de l’évolution de ces températures :
temp_moyennes |>
ggplot(aes(x = factor(month), y = moyenne)) +
geom_line(aes(group = 1)) +
geom_point() +
facet_wrap(~origin, ncol = 1) +
labs(x = "Mois",
y = "Moyenne des températures quotidiennes maximales (ºC)") +
theme_bw()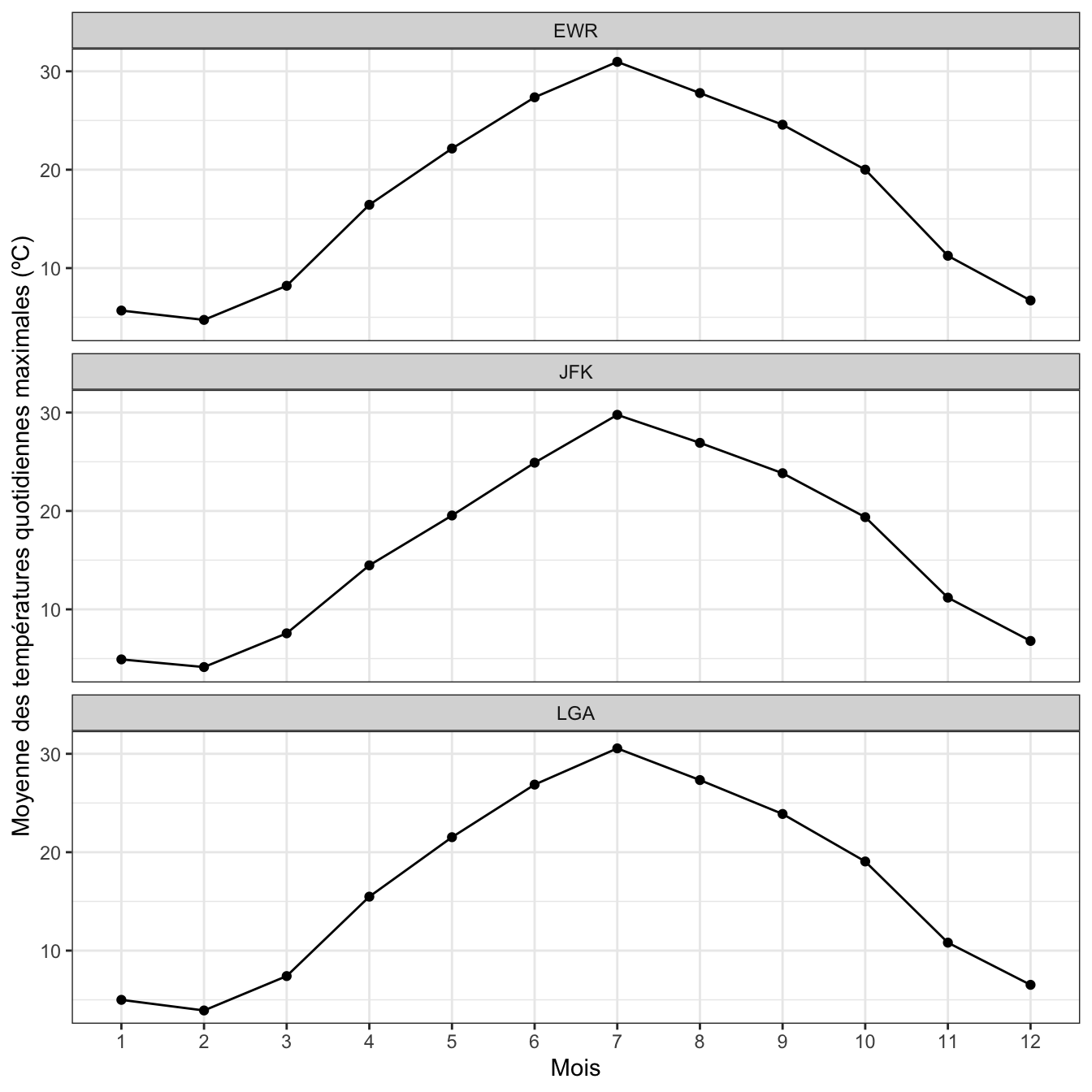
Vous remarquerez que :
- j’associe
factor(month), et non simplementmonth, à l’axe desxafin d’avoir, sur l’axe des abscisses, des chiffres cohérents allant de 1 à 12, et non des chiffres à virgule - l’argument
group = 1doit être ajouté pour que la ligne reliant les points apparaisse. En effet, les lignes sont censées relier des points qui appartiennent à une même série temporelle. Or ici, nous avons transformémonthen facteur. Précisergroup = 1permet d’indiquer àgeom_line()que toutes les catégories du facteurmonthappartiennent au même groupe, que ce facteur peut être considéré comme une variable continue, et qu’il est donc correct de relier les points.
Pour les 3 aéroports, les profils de températures sont très proches. C’est tout à fait logique puisqu’ils sont situés dans un rayon de quelques kilomètres seulement. Le problème de ce graphique est que chaque point a été obtenu en calculant une moyenne. En janvier, nous avons fait la moyenne de 31 valeurs de températures quotidiennes pour chaque aéroport. En février, nous avons fait la moyenne de 28 valeurs de températures quotidiennes pour chaque aéroport. Et ainsi de suite pour tous les mois de l’année 2013. Puisque nous présentons des valeurs de moyennes, il nous faut présenter également l’incertitude associée à ces calculs de moyennes. Pour cela, nous devons calculer l’erreur standard des moyennes :
temp_jour |>
summarise(moyenne = mean(temperature_max, na.rm = TRUE),
N_obs = n(),
erreur_standard = sd(temperature_max, na.rm = TRUE) / sqrt(N_obs),
.by = c(origin, month))# A tibble: 36 × 5
origin month moyenne N_obs erreur_standard
<chr> <int> <dbl> <int> <dbl>
1 EWR 1 5.69 31 1.14
2 EWR 2 4.74 28 0.762
3 EWR 3 8.20 31 0.649
4 EWR 4 16.4 30 0.919
5 EWR 5 22.2 31 1.02
6 EWR 6 27.4 30 0.769
7 EWR 7 31.0 31 0.700
8 EWR 8 27.8 31 0.385
9 EWR 9 24.6 30 0.716
10 EWR 10 20.0 31 0.882
# ℹ 26 more rowsNotre tableau de statistiques descriptives possède maintenant 2 colonnes supplémentaires : le nombre d’observations (que j’ai nommé N_obs), et l’erreur standard associée à chaque moyenne, calculée grâce à la formule vue plus haut \(se_{\bar{x}} = \frac{s}{\sqrt{n}}\) (la fonction sqrt() permet de calculer la racine carrée). On constate que l’erreur standard, qui s’exprime dans la même unité que la moyenne, est variable selon les mois de l’année. Ainsi, pour l’aéroport de Newark, l’incertitude semble particulièrement faible pour le mois d’août (0.385 ºC) mais presque 3 fois plus forte pour le mois de janvier (1.14 ºC).
Une fois de plus, je donne un nom à ce tableau de données pour pouvoir le réutiliser plus tard :
temperatures_se <- temp_jour |>
summarise(moyenne = mean(temperature_max, na.rm = TRUE),
N_obs = n(),
erreur_standard = sd(temperature_max, na.rm = TRUE) / sqrt(N_obs),
.by = c(origin, month))Notez que le package ggplot2 contient une fonction permettant de calculer à la fois la moyenne et erreur standard de la moyenne d’un échantillon : mean_se(). Puisque cette fonction renvoie 3 valeurs (\(\bar{x}\), \(\bar{x} - se\) et \(\bar{x} + se\)), on utilise reframe() :
temp_jour |>
reframe(mean_se(temperature_max),
.by = c(origin, month))# A tibble: 36 × 5
origin month y ymin ymax
<chr> <int> <dbl> <dbl> <dbl>
1 EWR 1 5.69 4.55 6.82
2 EWR 2 4.74 3.97 5.50
3 EWR 3 8.20 7.55 8.85
4 EWR 4 16.4 15.5 17.4
5 EWR 5 22.2 21.1 23.2
6 EWR 6 27.4 26.6 28.1
7 EWR 7 31.0 30.3 31.7
8 EWR 8 27.8 27.4 28.2
9 EWR 9 24.6 23.9 25.3
10 EWR 10 20.0 19.1 20.9
# ℹ 26 more rowsLes résultats obtenus ne sont pas exactement au même format :
- la colonne
ycontient les valeurs de moyennes (\(\bar{x}\)) - la colonne
ymincontient la valeur de moyenne moins une fois l’erreur standard (\(\bar{x} - se\)) - la colonne
ymaxcontient la valeur de moyenne plus une fois l’erreur standard (\(\bar{x} + se\))
Il ne nous restera plus qu’à ajouter des barres d’erreur sur notre graphique pour visualiser l’incertitude associée à chaque valeur de moyenne.
2.5 Calculs d’intervalles de confiance à 95%
Comme pour les erreurs standard, il est possible de calculer des intervalles de confiance de n’importe quel estimateur calculé à partir d’un échantillon, pour déterminer la gamme des valeurs les plus probables pour les paramètres équivalents dans la population générale. Nous nous concentrerons ici sur le calcul des intervalles de confiance à 95% de la moyenne, mais nous serons amenés à examiner également l’intervalle de confiance de la médiane, puis, au cours de votre L3, l’intervalle de confiance à 95% d’une différence de moyennes.
Contrairement à l’erreur standard, il n’y a pas qu’une bonne façon de calculer l’intervalle de confiance à 95% d’une moyenne. Plusieurs formules existent et le choix de la formule dépend en partie de la distribution des données (la distribution suit-elle une loi Normale ou non) et de la taille de l’échantillon dont nous disposons (\(n\) est-il supérieur à 30 ou non ?). Dans la situation idéale d’une variable qui suit la distribution Normale, les bornes inférieures et supérieures de l’intervalle de confiance à 95% sont obtenues grâce à cette formule
\[\bar{x} - 1.96 \cdot \frac{s}{\sqrt{n}} < \mu < \bar{x} + 1.96 \cdot \frac{s}{\sqrt{n}}\] Autrement dit, la vraie moyenne \(\mu\) d’une population a de bonnes chances de se trouver dans un intervalle de plus ou moins 1.96 fois l’erreur standard de la moyenne. En première approximation, l’intervalle de confiance est donc la moyenne de l’échantillon \(\bar{x}\) plus ou moins 2 fois l’erreur standard (que nous avons appris à calculer à la main un peu plus tôt). On peut donc calculer à la main les bornes inférieures et supérieures de l’intervalle de confiance ainsi :
temp_jour |>
reframe(mean_se(temperature_max, mult = 1.96),
.by = c(origin, month))# A tibble: 36 × 5
origin month y ymin ymax
<chr> <int> <dbl> <dbl> <dbl>
1 EWR 1 5.69 3.46 7.92
2 EWR 2 4.74 3.24 6.23
3 EWR 3 8.20 6.93 9.47
4 EWR 4 16.4 14.6 18.2
5 EWR 5 22.2 20.1 24.2
6 EWR 6 27.4 25.8 28.9
7 EWR 7 31.0 29.6 32.3
8 EWR 8 27.8 27.0 28.5
9 EWR 9 24.6 23.2 26.0
10 EWR 10 20.0 18.3 21.7
# ℹ 26 more rowsIci, grâce à l’argument mult = 1.96 de la fonction mean_se() :
- la colonne
ymincontient maintenant les valeurs de moyennes moins 1.96 fois l’erreur standard - la colonne
ymaxcontient maintenant les valeurs de moyennes plus 1.96 fois l’erreur standard
Dans la pratique, puisque cette méthode reste approximative et dépend de la nature des données dont on dispose, on utilisera plutôt des fonctions spécifiques qui calculeront pour nous les intervalles de confiance à 95% de nos estimateurs. C’est ce que permet en particulier la fonction mean_cl_normal() du package ggplot2. Il est toutefois important de bien comprendre qu’il y a un lien étroit entre l’erreur standard (l’incertitude associées à l’estimation d’un paramètre d’une population à partir des données d’un échantillon), et l’intervalle de confiance à 95% de ce paramètre.
temp_jour |>
reframe(mean_cl_normal(temperature_max),
.by = c(origin, month))# A tibble: 36 × 5
origin month y ymin ymax
<chr> <int> <dbl> <dbl> <dbl>
1 EWR 1 5.69 3.36 8.01
2 EWR 2 4.74 3.17 6.30
3 EWR 3 8.20 6.88 9.53
4 EWR 4 16.4 14.6 18.3
5 EWR 5 22.2 20.1 24.2
6 EWR 6 27.4 25.8 28.9
7 EWR 7 31.0 29.5 32.4
8 EWR 8 27.8 27.0 28.6
9 EWR 9 24.6 23.1 26.0
10 EWR 10 20.0 18.2 21.8
# ℹ 26 more rowsComme dans les tableaux précédents, 3 nouvelles colonnes ont été crées :
ycontient toujours la moyenne des températures mensuelles pour chaque aéroportymincontient maintenant les bornes inférieures de l’intervalle à 95% des moyennesymaxcontient maintenant les bornes supérieures de l’intervalle à 95% des moyennes
Pour que la suite soit plus claire, nous allons afficher et donner des noms à ces différents tableaux en prenant soin de renommer les colonnes pour plus de clarté.
Tout d’abord, nous disposons du tableau temperatures_se, qui contient, les moyennes des températures mensuelles de chaque aéroport de New York en 2013, et les erreurs standard de ces moyennes :
temperatures_se# A tibble: 36 × 5
origin month moyenne N_obs erreur_standard
<chr> <int> <dbl> <int> <dbl>
1 EWR 1 5.69 31 1.14
2 EWR 2 4.74 28 0.762
3 EWR 3 8.20 31 0.649
4 EWR 4 16.4 30 0.919
5 EWR 5 22.2 31 1.02
6 EWR 6 27.4 30 0.769
7 EWR 7 31.0 31 0.700
8 EWR 8 27.8 31 0.385
9 EWR 9 24.6 30 0.716
10 EWR 10 20.0 31 0.882
# ℹ 26 more rowsEnsuite, nous avons produit un tableau presque équivalent que nous allons nommer temperature_se_bornes et pour lequel nous allons modifier le nom des colonnes y, ymin et ymax :
temperature_se_bornes <- temp_jour |>
reframe(mean_se(temperature_max),
.by = c(origin, month)) |>
rename(moyenne = y,
moyenne_moins_se = ymin,
moyenne_plus_se = ymax)
temperature_se_bornes# A tibble: 36 × 5
origin month moyenne moyenne_moins_se moyenne_plus_se
<chr> <int> <dbl> <dbl> <dbl>
1 EWR 1 5.69 4.55 6.82
2 EWR 2 4.74 3.97 5.50
3 EWR 3 8.20 7.55 8.85
4 EWR 4 16.4 15.5 17.4
5 EWR 5 22.2 21.1 23.2
6 EWR 6 27.4 26.6 28.1
7 EWR 7 31.0 30.3 31.7
8 EWR 8 27.8 27.4 28.2
9 EWR 9 24.6 23.9 25.3
10 EWR 10 20.0 19.1 20.9
# ℹ 26 more rowsNous avons ensuite calculé manuellement des intervalles de confiance approximatifs, avec la fonction mean_se() et son argument mult = 1.96. Là encore, nous allons stocker cet objet dans un tableau nommé temperatures_ci_approx, et nous allons modifier le nom des colonnes y, ymin, et ymax :
temperature_ci_approx <- temp_jour |>
reframe(mean_se(temperature_max, mult = 1.96),
.by = c(origin, month)) |>
rename(moyenne = y,
ci_borne_inf = ymin,
ci_borne_sup = ymax)
temperature_ci_approx# A tibble: 36 × 5
origin month moyenne ci_borne_inf ci_borne_sup
<chr> <int> <dbl> <dbl> <dbl>
1 EWR 1 5.69 3.46 7.92
2 EWR 2 4.74 3.24 6.23
3 EWR 3 8.20 6.93 9.47
4 EWR 4 16.4 14.6 18.2
5 EWR 5 22.2 20.1 24.2
6 EWR 6 27.4 25.8 28.9
7 EWR 7 31.0 29.6 32.3
8 EWR 8 27.8 27.0 28.5
9 EWR 9 24.6 23.2 26.0
10 EWR 10 20.0 18.3 21.7
# ℹ 26 more rowsEnfin, nous avons calculé les intervalles de confiance avec une fonction spécialement dédiée à cette tâche : la fonction mean_cl_normal(). Nous allons stocker cet objet dans un tableau nommé temperatures_ci, et nous allons modifier le nom des colonnes y, ymin, et ymax :
temperature_ci <- temp_jour |>
reframe(mean_cl_normal(temperature_max),
.by = c(origin, month)) |>
rename(moyenne = y,
ci_borne_inf = ymin,
ci_borne_sup = ymax)
temperature_ci# A tibble: 36 × 5
origin month moyenne ci_borne_inf ci_borne_sup
<chr> <int> <dbl> <dbl> <dbl>
1 EWR 1 5.69 3.36 8.01
2 EWR 2 4.74 3.17 6.30
3 EWR 3 8.20 6.88 9.53
4 EWR 4 16.4 14.6 18.3
5 EWR 5 22.2 20.1 24.2
6 EWR 6 27.4 25.8 28.9
7 EWR 7 31.0 29.5 32.4
8 EWR 8 27.8 27.0 28.6
9 EWR 9 24.6 23.1 26.0
10 EWR 10 20.0 18.2 21.8
# ℹ 26 more rowsMaintenant, si l’on compare les 2 tableaux contenant les calculs d’intervalles de confiance de la moyenne, on constate que les résultats sont très proches :
temperature_ci_approx
temperature_ci# A tibble: 36 × 5
origin month moyenne ci_borne_inf ci_borne_sup
<chr> <int> <dbl> <dbl> <dbl>
1 EWR 1 5.69 3.46 7.92
2 EWR 2 4.74 3.24 6.23
3 EWR 3 8.20 6.93 9.47
4 EWR 4 16.4 14.6 18.2
5 EWR 5 22.2 20.1 24.2
6 EWR 6 27.4 25.8 28.9
7 EWR 7 31.0 29.6 32.3
8 EWR 8 27.8 27.0 28.5
9 EWR 9 24.6 23.2 26.0
10 EWR 10 20.0 18.3 21.7
# ℹ 26 more rows# A tibble: 36 × 5
origin month moyenne ci_borne_inf ci_borne_sup
<chr> <int> <dbl> <dbl> <dbl>
1 EWR 1 5.69 3.36 8.01
2 EWR 2 4.74 3.17 6.30
3 EWR 3 8.20 6.88 9.53
4 EWR 4 16.4 14.6 18.3
5 EWR 5 22.2 20.1 24.2
6 EWR 6 27.4 25.8 28.9
7 EWR 7 31.0 29.5 32.4
8 EWR 8 27.8 27.0 28.6
9 EWR 9 24.6 23.1 26.0
10 EWR 10 20.0 18.2 21.8
# ℹ 26 more rowsLes bornes inférieures et supérieures des intervalles de confiance à 95% des moyennes ne sont pas égales quand on les calcule manuellement de façon approchée et quand on les calcule de façon exacte, mais les différences sont minimes.