3 Séances 1 et 2 : statistiques descriptives et tests d’hypothèses

3.1 Packages et données

Pour chacune des 4 séances de travaux pratiques (et TEA) qui viennent, vous aurez besoin d’utiliser des packages spécifiques et d’importer des données depuis des fichiers externes disponibles sur l’ENT (ou directement depuis ce document).

Les packages dont vous aurez besoin pour cette séance, et que vous devez donc charger en mémoire, sont les packages du tidyverse (Wickham, 2021), qui permettent de manipuler facilement des tableaux de données et de réaliser des graphiques, le package readr (Wickham, Hester, et al., 2022), pour importer facilement des fichiers .csv au format tibble, le package readxl (Wickham & Bryan, 2022), pour importer facilement des fichiers Excel au format tibble, le package skimr (Waring et al., 2021), qui permet de calculer des résumés de données très informatifs, et le package car (Fox et al., 2021), qui permet d’effectuer le test de comparaison des variances de Levene :

library(tidyverse)
library(readr)
library(readxl)
library(skimr)
library(car)

Si ces commandes (que vous devez taper dans vos scripts avant de les exécuter dans la console de RStudio) renvoient des messages d’erreur, c’est que les packages que vous essayez de charger en mémoire ne sont pas installés sur votre ordinateur. Il vous faudra alors installer les packages manquants avec la fonction :

install.packages("nom_du_package")

Comme d’habitude, si tout ça est un peu flou pour vous, relisez la section 2.3 du livre de biométrie 2 disponible en ligne.

Vous aurez également besoin des jeux de données suivants :

3.2 Comparaison de la moyenne d’une population à une valeur théorique

3.2.1 Exploration préalable des données

Avant de se lancer dans les tests d’hypothèses, il est toujours indispensable d’examiner les données dont on dispose à l’aide, d’une part de statistiques descriptives numériques, et d’autres part, de graphiques exploratoires. Nous allons voir dans cette section quels indices statistiques il peut être utile de calculer et quelles représentations graphiques il peut être utile de réaliser afin de pouvoir se lancer dans des tests d’hypothèses sans risquer de grossières erreurs.

3.2.1.1 Importation et examen visuel

Commencez par importer les données contenues dans le fichier Temperature.csv. Pour cela, utilisez l’assistant d’importation de RStudio. Si vous ne savez plus comment faire, consultez la section 5.3 du livre en ligne de Biométrie 2.

Vous stockerez les données dans un objet que vous nommerez Temperature. Après l’importation, taper son nom dans la console de RStudio doit produire le résultat suivant :

Temperature

# A tibble: 25 × 2
   individual temperature
        <dbl>       <dbl>
 1          1        98.4
 2          2        98.6
 3          3        97.8
 4          4        98.8
 5          5        97.9
 6          6        99  
 7          7        98.2
 8          8        98.8
 9          9        98.8
10         10        99  
# … with 15 more rows

Ce tableau contient les températures corporelles de 25 adultes en bonne santé choisis au hasard parmi la population américaine. On souhaite examiner la croyance populaire indiquant que la température moyenne d’adultes en bonne santé vaut 37ºC.

La première chose à faire quand on travaille avec des données inconnues, c’est d’examiner les données brutes. Ici, les données sont importées au format tibble, donc seules les premières lignes sont visibles. Pour visualiser l’ensemble du tableau, utilisez la fonction View() :

View(Temperature)

Cette commande doit ouvrir un nouvel onglet présentant les données dans un tableur simplifié, en lecture seule.

On constate ici 2 choses que nous allons modifier :

la première colonne, intitulée individual, n’est pas véritablement une variable. Cette colonne ne contient qu’un identifiant qui est en fait identique au numéro de ligne. Nous allons donc supprimer cette colonne
les températures sont exprimées en degrés Fahrenheit, ce qui rend leur lecture difficile pour nous qui sommes habitués à utiliser le système métrique et les degrés Celsius. Nous allons donc convertir les températures en degrés Celsius grâce à la formule suivante :

\[ºC = \frac{ºF - 32}{1.8}\]

Temp_clean <- Temperature %>% 
  select(-individual) %>%      # Suppression de la première colonne
  mutate(                      # Transformation des températures en Celsius
    temperature = (temperature - 32) / 1.8
    )

Temp_clean

# A tibble: 25 × 1
   temperature
         <dbl>
 1        36.9
 2        37  
 3        36.6
 4        37.1
 5        36.6
 6        37.2
 7        36.8
 8        37.1
 9        37.1
10        37.2
# … with 15 more rows

Il nous est maintenant possible d’examiner à nouveau les données avec la fonction View(). Avec des valeurs de températures comprises entre 36.3 ºC et 37.8 ºC, il n’y a visiblement pas de données aberrantes.

C’est toujours la première chose à faire : regarder les données brutes pour repérer :

La nature des variables présentes.
Les variables inutiles qui pourront être supprimées ou négligées.
Les unités des variables utiles, afin de pouvoir les convertir si nécessaire.
Les valeurs manquantes ou aberrantes qui demanderont toujours une attention particulière.

Une fois l’examen préliminaire des données réalisé, on peut passer au calcul des statistiques descriptives.

3.2.1.2 Statistiques descriptives

On s’intéresse ici au calcul de grandeurs statistiques nous apportant des renseignements sur la distribution des valeurs de l’échantillon. Les questions auxquelles on tente de répondre à ce stade sont les suivantes :

Quelle est la tendance moyenne ?
Quelle est la dispersion des données autour de la moyenne ?

Pour répondre à ces questions, on peut faire appel à de multiples fonctions. J’en évoquerai ici seulement 3 qui permettent d’obtenir la plupart des informations dont nous avons besoin très simplement :

summary(Temp_clean)

  temperature   
 Min.   :36.33  
 1st Qu.:36.67  
 Median :37.00  
 Mean   :36.96  
 3rd Qu.:37.22  
 Max.   :37.78

Comme son nom l’indique, la fonction summary() renvoie un résumé des données :

les valeurs extrêmes (minimum et maximum)
les valeurs “centrales” (moyenne et médiane)
les valeurs des quartiles (premier et troisième quartiles)

Ces valeurs seront presques toutes reprises sur le graphique de type “boîte à moustaches” que nous verrons plus bas.

On constate ici que la moyenne et la médiane sont très proches. La distribution des températures doit donc être à peut près symmétrique, avec à peu près autant de valeurs au-dessus que de valeurs en dessous de la moyenne.

La seconde fonction utile est la fonction IQR(), comme “Inter Quartile Range” (ou intervalle inter-quartile). Cette fonction renvoie l’étendue de l’intervalle inter-quartile, c’est à dire la valeur du troisième quartile moins la valeur de premier quartile. Attention, cette fonction a besoin d’un vecteur en guise d’argument, or nos données sont stockées sous forme de tibble. Nous allons donc utiliser la fonction pull() du package dplyr afin de transformer (momentanément) la colonne temperature du tableau Temp_clean en vecteur :

Temp_clean %>% 
  pull(temperature) %>% 
  IQR()

[1] 0.5555556

On constate ici que l’intervalle inter quartile a une largeur de 0.55 degrés Celsius. Cela signifie que les 50% des températures les plus centrales sont situées dans un intervalle d’environ un demi-degré celsius.

Enfin, une autre façon d’obtenir des informations rapidement consiste à utiliser la fonction skim() du package skimr :

skim(Temp_clean)

── Data Summary ────────────────────────
                           Values    
Name                       Temp_clean
Number of rows             25        
Number of columns          1         
_______________________              
Column type frequency:               
  numeric                  1         
________________________             
Group variables            None      

── Variable type: numeric ──────────────────────────────────────────────────────
  skim_variable n_missing complete_rate  mean    sd    p0   p25   p50   p75
1 temperature           0             1  37.0 0.377  36.3  36.7    37  37.2
   p100 hist 
1  37.8 ▇▇▇▇▂

Tout comme summary(), la fonction skim() renvoie les valeurs minimales et maximales, les premiers et troisièmes quartiles ainsi que la moyenne et la médiane. Elle nous indique en outre la valeur de l’écart-type de l’échantillon, ainsi que le nombre d’observations et le nombre de données manquantes. Enfin, elle fournit un histogramme très schématique et sans échelle. Cet histogramme nous permet de nous faire une première idée de la distribution des données.

Outre ces 3 fonctions (summary(), IQR(), et skim()), il est bien sûr possible de calculer toutes ces valeurs manuellement si besoin :

mean() permet de calculer la moyenne.
median() permet de calculer la médiane.
min() et max() permettent de calculer les valeurs minimales et maximales respectivement.
quantile() permet de calculer les quartiles.
sd() permet de calculer l’écart-type.
var() permet de calculer la variance.

Toutes ces fonctions prennent seulement un vecteur en guise d’argument. Il faut donc procéder comme avec IQR() pour les utiliser. Par exemple, pour calculer la variance, on peut taper :

Temp_clean %>% 
  pull(temperature) %>% 
  var()

[1] 0.1417901

ou :

var(Temp_clean$temperature)

[1] 0.1417901

3.2.1.3 Exploration graphique

Ici, il s’agit d’examiner la distribution des données. Pour cela, 3 types de graphiques sont généralement utilisés.

Les nuages de points ou stripcharts :

Temp_clean %>% 
  ggplot(aes(x = 1, y = temperature)) +
  geom_point()

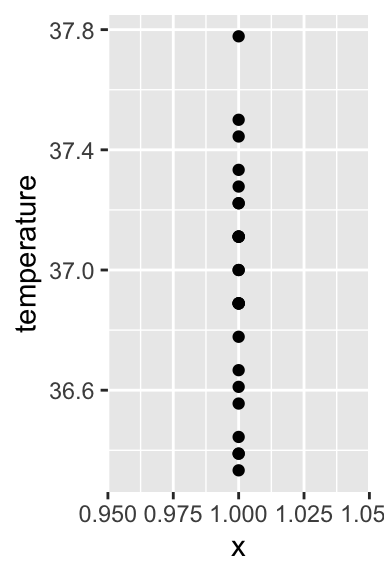
Dans la mesure où souvent, plusieurs observations ont la même valeur, il faut tenir compte de l’over-plotting. Si vous ne vous rappelez plus de quoi il s’agit, consultez la section 4.3.4 du livre en ligne de Biométrie 2. Globalement, pour visualiser correctement les données, on va jouer soit sur la transparence des points, soit sur l’ajout d’un bruit aléatoire horizontal qui permettra de distinguer plus facilement les points et de repérer les zones où les points sont abondants ou rares :

Temp_clean %>% 
  ggplot(aes(x = 1, y = temperature)) +
  geom_jitter(height = 0, width = 0.1) +
  xlim(0.5, 1.5)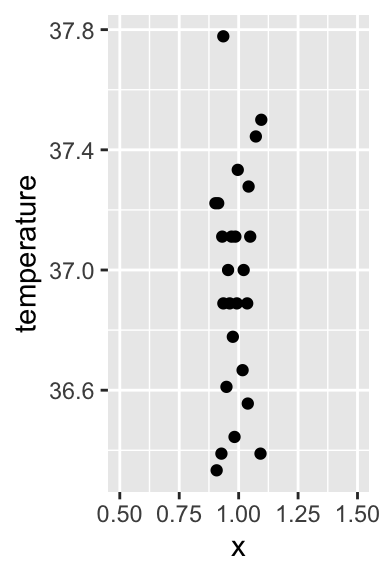

La fonction xlim() permet de spécifier manuellement les valeurs limites que l’on souhaite pour l’axe des abscisses. Ici, cet axe n’a aucune signification particulière puisque nous n’avons qu’une unique série de données (c’est la raison pour laquelle les points sont centrés sur l’abscisse x = 1). Nous pouvons donc le masquer comme ceci :

Temp_clean %>% 
  ggplot(aes(x = 1, y = temperature)) +
  geom_jitter(height = 0, width = 0.1) +
  xlim(0.5, 1.5) +
  theme(axis.text.x = element_blank(),
        axis.ticks.x = element_blank(),
        axis.title.x = element_blank())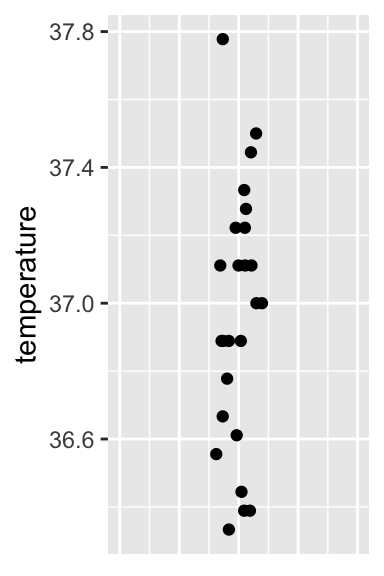

On constate ici que la répartition des points est assez régulière, avec néanmoins une majorité de points entre 36.8 et 37.3 degrés Celsius.

L’histogramme :

Temp_clean %>% 
  ggplot(aes(x = temperature)) +
  geom_histogram(bins = 10, color = grey(0.8))

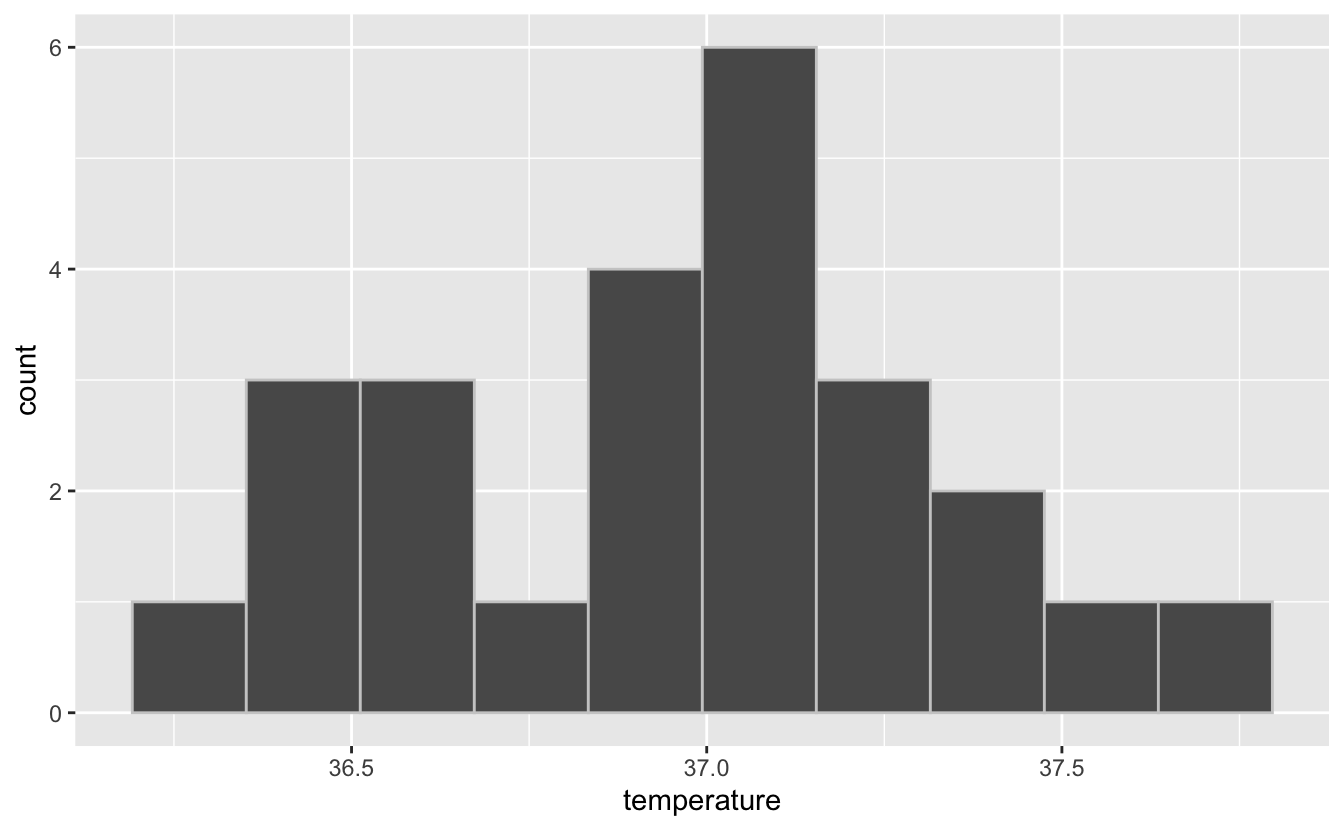
Si vous ne vous rappelez-plus ce qu’est un histogramme ou comment le faire, ou la signification de l’argument bins, relisez la section 4.5 du livre en ligne de Biométrie 2.

Notez ici que la forme de cet histogramme est relativement proche de celle présentée plus tôt par la fonction skim(). Cet histogramme nous apprend qu’en dehors d’un “trou” autour de la température 36.75 ºC, la distribution des données est proche d’une courbe en cloche. Il y a fort à parier qu’un test de normalité concluerait à la normalité des données de cet échantillon.

Les boîtes à moustaches :

Temp_clean %>% 
  ggplot(aes(y = temperature)) +
  geom_boxplot(notch = TRUE)

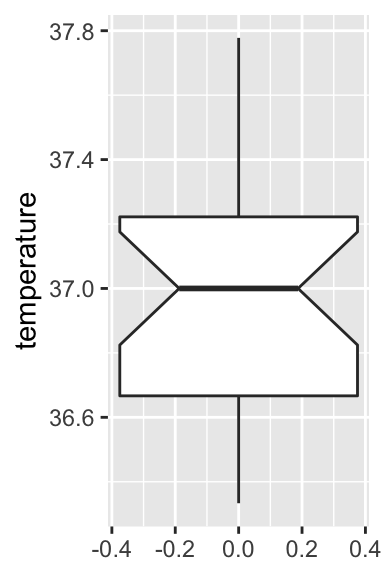
Comme pour le stripchart présenté plus haut, l’axe des abscisses n’a ici aucun sens. Nous n’avons qu’une unique série de données, l’axe des x est donc inutile et nous pouvons donc le retirer :

Temp_clean %>% 
  ggplot(aes(y = temperature)) +
  geom_boxplot(notch = TRUE) +
  theme(axis.text.x = element_blank(),
        axis.ticks.x = element_blank())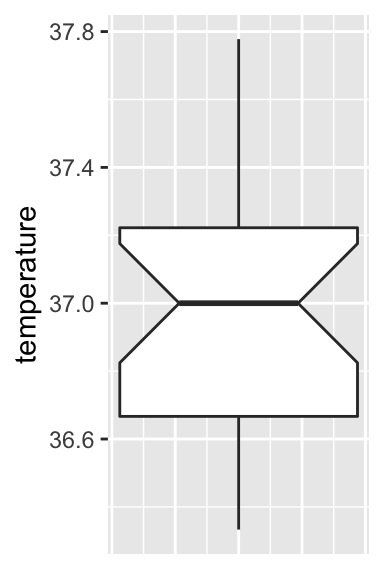

On retrouve sur ce graphique tous les éléments obtenus avec la fonction summary() à l’exception de la moyenne. Assurez-vous que vous êtes bien capables d’identifier tous ces éléments sur le graphique. Assurez-vous aussi que la signification de l’encoche (obtenue avec l’argument notch = TRUE) est bien claire pour vous. Comme toujours, si ce n’est pas le cas, consultez la section dédiée aux boxplots dans le livre en ligne de Biométrie 2.

Pour conclure, ces 3 types de représentations graphiques (nuages de points ou stripchart, histogrammes et boxplots) sont complémentaires. Ces trois types de représentations graphiques permettent de visualiser la distribution d’une variable numérique. Les nuages de points permettent de voir toutes les données brutes. Les histogrammes résument les données en quelques valeurs : une valeur d’abondance pour chaque barre ou classe. Les boxplots résument encore plus les données avec seulement 7 valeurs qui caractérisent la distribution (voir figure 3.1 ci-dessous).

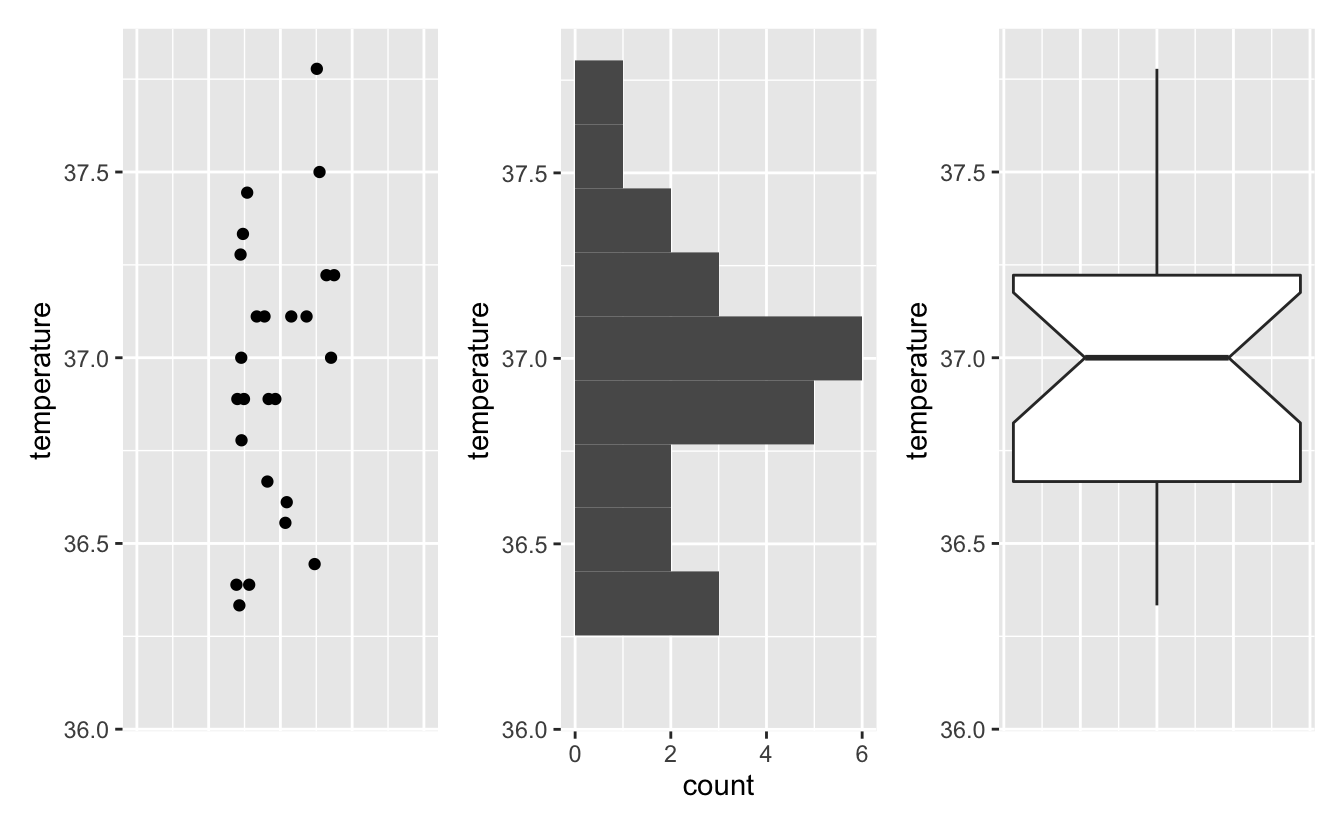
Figure 3.1: Comparaison de 2 types de représentations graphiques

À chaque nouvelle analyse statistique, il sera donc important de visualiser les données afin de repérer les éventuels problèmes et afin d’anticiper sur les résultats que fourniront les tests d’hypothèses ultérieurs. Ici, l’examen de ces graphiques nous permet de dire les choses suivantes :

Il n’y a visiblement pas de données aberrantes.
La distribution des données semble suivre à peu près la loi Normale.
La médiane et son intervalle de confiance à 95% sont centrés sur la valeur 37ºC. Un test devrait donc arriver à la conclusion que la température corporelle des adultes n’est pas significativement différente de 37ºC. Néanmoins, la largeur de l’intervalle de confiance à 95% est assez grande, ce qui indique une incertitude relativement élevée. Une plus grande quantité de données permettrait certainement d’obtenir plus de précision.

3.2.2 Le test paramétrique

Le test permettant de comparer la moyenne d’une population à une valeur théorique, fixée par l’utilisateur, est le test de Student à un échantillon. Il s’agit d’un test paramétrique très puissant. Comme tous les tests paramétriques, certaines conditions d’application doivent être vérifiées avant de pouvoir l’appliquer.

3.2.2.1 Conditions d’application

Les conditions d’application du test de Student à un échantillon sont les suivantes :

Les données de l’échantillon sont issues d’un échantillonnage aléatoire au sein de la population générale. Cette condition est partagée par toutes les méthodes que nous verrons dans ces TP. En l’absence d’informations sur la façon dont l’échantillonnage a été réalisé, on considère que cette condition est remplie. Il n’y a pas de moyen statistique de le vérifier, cela fait uniquement référence à la stratégie d’échantillonnage et à la rigueur de la procédure mise en œuvre lors de l’acquisition des données.
La variable étudiée doit suivre une distribution Normale dans la population générale. Nous allons vérifier cette condition d’application avec un test de normalité de Shapiro-Wilk.

Comme pour tous les tests statistiques que nous allons réaliser lors de ces séances de TP et TEA, nous devons commencer par spécifier les hypothèses nulles et alternatives ainsi que la valeur du seuil $\alpha$ que nous allons utiliser. Ici, nous utiliserons toujours le seuil $\alpha = 0.05$.

Pour un test de normalité, les hypothèses sont toujours les suivantes :

H$_0$ : la variable étudiée suit une distribution Normale dans la population générale.
H$_1$ : la variable étudiée ne suit pas une distribution Normale dans la population générale.

Le test de Shapiro-Wilk se réalise de la façon suivante :

Temp_clean %>% 
  pull(temperature) %>% 
  shapiro.test()


    Shapiro-Wilk normality test

data:  .
W = 0.97216, p-value = 0.7001

W est la statistique du test. Elle permet à RStudio de calculer la p-value du test. Ici, $p > \alpha$. On ne peut donc pas rejeter l’hypothèse nulle de normalité : on ne peut pas exclure que dans la population générale, la température suive bel et bien une distribution Normale. Les conditions d’application du test de Student sont bien vérifiées.

3.2.2.2 Réalisation du test et interprétation

Puisque les conditions d’application du test de Student à un échantillon sont vérifiées, nous devons maintenant spécifier les hypothèses nulles et alternatives que nous allons utiliser pour réaliser ce test :

H$_0$ : dans la population générale, la température corporelle moyenne des adultes en bonne santé vaut 37ºC ($\mu = 37$).
H$_1$ : dans la population générale, la température corporelle moyenne des adultes en bonne santé est différente de 37ºC ($\mu \neq 37$).

On réalise ensuite le test de la façon suivante :

Temp_clean %>% 
  pull(temperature) %>% 
  t.test(mu = 37)


    One Sample t-test

data:  .
t = -0.56065, df = 24, p-value = 0.5802
alternative hypothesis: true mean is not equal to 37
95 percent confidence interval:
 36.80235 37.11321
sample estimates:
mean of x 
 36.95778

Sur la première ligne, R nous confirme que nous avons bien réalisé un test de Student à un échantillon. La première ligne de résultats fournit la valeur du $t$ calculé (ici, -0.56), le nombre de degrés de libertés (ici, df = 24), et la $p$-value (ici, 0.58, soit une valeur supérieure à $\alpha$). Cette première ligne contient donc tous les résultats du test qu’il conviendrait de rappeler dans un rapport. On devrait ainsi dire :

Au seuil $\alpha$ de 5%, on ne peut pas rejeter l’hypothèse nulle $\mu = 37$ ($t = -0.56$, ddl = 24, $p = 0.58$). Les données observées sont donc compatibles avec l’hypothèse selon laquelle la température corporelle moyenne des adultes en bonne santé vaut 37ºC.

C’est de cette manière que vous devriez rapporter les resultats de ce test dans vos comptes-rendus et rapports à partir de maintenant.

Dans les résultats du test, la ligne suivante (alternative hypothesis: ...) ne donne pas la conclusion du test. Il s’agit simplement d’un rappel concernant l’hypothèse alternative qui a été utilisée pour réaliser le test. Ici, l’hypothèse alternative utilisée est une hypothèse bilatérale ($\mu \neq 37$). Nous verrons plus tard comment spécifier des hypothèses alternatives uni-latérales, même si la plupart du temps, mieux vaut s’abstenir de réaliser de tels tests (à moins bien sûr d’avoir une bonne raison de le faire).

Les résultats fournis ensuite concernent, non plus le test statistique à proprement parler, mais l’estimation. Ici, la moyenne de l’échantillon est fournie. Il s’agit de la meilleure estimation possible de la moyenne de la population : $\bar{x} = \hat{\mu} = 36.96$. Comme pour toutes les estimations, cette valeur est entachée d’incertitude liée à la fluctuation d’échantillonnage. L’intervalle de confiance à 95% de cette estimation de moyenne est donc également fourni : $[36.80 ; 37.11]$. Autrement dit, cet intervalle contient les valeurs les plus vraissemblables pour la véritable valeur de moyenne dans la population générale. Cela confirme bien que nous n’avons pas prouvé au sens strict que la moyenne de la population vaut 37ºC. Nous avons en réalité montré que nous ne pouvions pas exclure que la moyenne de la population générale soit de 37ºC. Cette valeur est en effet comprise dans l’intervalle de confiance. On ne peut donc pas l’exclure : nos données sont compatibles avec cette hypothèse. Mais beaucoup d’autres valeurs figurent aussi dans cet intervalle. Il est donc tout à fait possible que la moyenne soit en réalité différente de 37ºC. Pour en être sûr, il faudrait probablement un échantillon de plus grande taille afin de limiter l’incertitude.

3.2.3 L’alternative non paramétrique

Si jamais les conditions d’application du test de Student à un échantillon n’étaient pas remplies, il faudrait alors réaliser son équivalent non paramétrique : le test de Wilcoxon des rangs signés. Ce test est moins puissant que son homologue paramétrique. On ne l’effectue donc que lorsque l’on n’a pas le choix :

Temp_clean %>% 
  pull(temperature) %>% 
  wilcox.test(mu = 37, conf.int = TRUE)

Warning in wilcox.test.default(., mu = 37, conf.int = TRUE): cannot compute
exact p-value with ties

Warning in wilcox.test.default(., mu = 37, conf.int = TRUE): cannot compute
exact confidence interval with ties


    Wilcoxon signed rank test with continuity correction

data:  .
V = 143, p-value = 0.6077
alternative hypothesis: true location is not equal to 37
95 percent confidence interval:
 36.77780 37.11114
sample estimates:
(pseudo)median 
      36.94446

La syntaxe est identique à celle du test de Student à un échantillon à une exception près : l’ajout de l’argument conf.int = TRUE qui permet d’afficher la (pseudo)médiane de l’échantillon et son intervalle de confiance à 95%.

Les hypothèses nulles et alternatives de ce test sont les mêmes que celles du test de Student à un échantillon. En toute rigueur, on teste l’égalité de la médiane à une valeur théorique, et non l’égalité de la moyenne. Mais dans la pratique, la grande majorité des utilisateurs de ce test font l’amalgame entre moyenne et médiane. Ici, la conclusion correcte devrait être :

Au seuil $\alpha$ de 5%, on ne peut pas rejeter l’hypothèse nulle (test de Wilcoxon des rangs signés, $V$ = 143, $p$ = 0.6077). La médiane de la population ($\widehat{med}$ = 36.94) n’est pas significativement différente de 37ºC (IC 95% : $[36.78 ; 37.11]$).

Si les données ne suivent pas la loi Normale, la médiane est bien la métrique la plus intéressante puisque c’est elle qui nous renseigne sur la tendance centrale des données.

Enfin, les tests de Wilcoxon renvoient souvent des messages d’avretissement. Il ne s’agit que de ça : des avertissements. Tant que la $p$-value des tests est éloignée de la valeur seuil $\alpha$, cela n’a pas d’importance. Quand en revanche la $p$-value est très proche de $\alpha$, il faut être très prudent face aux conclusions du test qui peuvent alors être assez “fragiles”.

(Notez que pour le test de Student à un échantillon comme pour le test de Wilcoxon des rangs signés, les conclusions sont en accord avec nos observations initiales réalisées à partir du boxplot).

3.2.4 Exercice d’application

Le fichier Temperature2.csv contient les données brutes d’une seconde étude similaire, réalisée à plus grande échelle. Importez ces données et analysez-les afin de vérifier si la température corporelle moyenne des adultes en bonne santé vaut bien 37ºC. Comme toujours, avant de vous lancer dans la réalisation des tests statistiques, prenez le temps d’examiner vos données comme nous l’avons décrit dans la section 3.2.1, afin de savoir où vous allez, et de repérer les éventuelles données manquantes ou aberrantes.

3.3 Comparaison de la moyenne de 2 populations : données appariées

On s’intéresse ici à la comparaison de 2 séries de données dont les observations sont liées 2 à 2. C’est par exemple le cas lorsque l’on fait subir un traitement à différents sujets et que l’on souhaite comparer les mesures obtenues avant et après le traitement.

Autrement dit, dans les plans d’expériences appariés, les deux traitements ou modalités sont appliqués à chaque unité d’échantillonnage.

Voici quelques exemples de situations qui devraient être traitées avec des tests sur données appariées :

Comparaison de la masse de patients avant et après une hospitalisation.
Comparaison de la diversité de peuplements de poissons dans des lacs avant et après contamination par des métaux lourds.
Test des effets d’une crème solaire appliquée sur un bras de chaque volontaire alors que l’autre bras ne reçoit qu’un placébo.
Test des effets du tabagisme dans un échantillon de fumeurs, dont chaque membre est comparé à un non fumeur choisi pour qu’il lui ressemble le plus possible en terme d’âge, de masse, d’origine éthnique et sociale, etc.
Test des effets que les conditions socio-économiques ont sur les préférences alimentaires en comparant des vrais jumaux élevés dans des familles adoptives séparées qui diffèrent en termes de conditions socio-économiques.

Les 2 derniers exemples montrent que même des individus séparés peuvent constituer une “paire statistique” s’ils partagent un certain nombre de caractéristiques (physiques, environnementales, génétiques, comportementales, etc.) pertinentes pour l’étude.

3.3.1 Exploration préalable des données

Ici, nous allons nous intéresser au lien qui pourrait exister entre la production de testostérone et l’immunité chez une espèce d’oiseau vivant en Amérique du Nord, le carouge à épaulettes.

Chez de nombreuses espèces, les mâles ont plus de chances d’attirer des femelles s’ils produisent des niveaux de testostérone élevés. Est-ce que la forte production de testostérone de certains mâles a un coût, notamment en terme d’immuno-compétence ? Autrement dit, est-ce que produire beaucoup de testostérone au moment de la reproduction (ce qui fournit un avantage sélectif) se traduit par une immunité plus faible par la suite, et donc une plus forte susceptibilité de contracter des maladies (ce qui constitue donc un désavantage sélectif) ?

Pour étudier cette question, une équipe de chercheurs (Hasselquist et al., 1999) a mis en place le dispositif expérimental suivant. Les niveaux de testostérone de 13 carouges à épaulettes mâles ont été artificiellement augmentés par l’implantation chirurgicale d’un microtube perméable contenant de la testostérone. L’immunocompétence a été mesurée pour chaque oiseau avant et après l’opération chirurgicale. La variable mesurée est la production d’anticorps suite à l’exposition des oiseaux avec un antigène non pathogène mais censé déclencher une réponse immunitaire. Les taux de production d’anticorps sont exprimés en logarithmes de densité optique par minute $\left(\ln\frac{mOD}{min}\right)$.

3.3.1.1 Importation et examen visuel

Les données se trouvent dans le fichier Testosterone.csv. Importez ces données dans un objet nommé Testo et examinez le tableau obtenu.

Testo

# A tibble: 13 × 5
   blackbird beforeImplant afterImplant logBeforeImplant logAfterImplant
       <dbl>         <dbl>        <dbl>            <dbl>           <dbl>
 1         1           105           85             4.65            4.44
 2         2            50           74             3.91            4.3 
 3         3           136          145             4.91            4.98
 4         4            90           86             4.5             4.45
 5         5           122          148             4.8             5   
 6         6           132          148             4.88            5   
 7         7           131          150             4.88            5.01
 8         8           119          142             4.78            4.96
 9         9           145          151             4.98            5.02
10        10           130          113             4.87            4.73
11        11           116          118             4.75            4.77
12        12           110           99             4.7             4.6 
13        13           138          150             4.93            5.01

Visiblement, il n’y a pas de données manquantes mais certaines variables sont inutiles. En réalité, nous aurons besoin des données sous 2 formats disctincts : un format “large” pour les statistiques descriptives et les tests d’hypothèses, et un format “long” pour les représentations graphiques. Et dans tous les cas, l’identifiant individuel devrait être considéré comme un facteur, et non comme une variable numérique comme c’est le cas actuellement.

Commençons par créer un tableau “large” pour les statistiques descriptives :

Testo_large <- Testo %>% 
  mutate(blackbird = factor(blackbird)) %>%
  select(ID = blackbird,
         Before = logBeforeImplant,
         After = logAfterImplant)

Testo_large

# A tibble: 13 × 3
   ID    Before After
   <fct>  <dbl> <dbl>
 1 1       4.65  4.44
 2 2       3.91  4.3 
 3 3       4.91  4.98
 4 4       4.5   4.45
 5 5       4.8   5   
 6 6       4.88  5   
 7 7       4.88  5.01
 8 8       4.78  4.96
 9 9       4.98  5.02
10 10      4.87  4.73
11 11      4.75  4.77
12 12      4.7   4.6 
13 13      4.93  5.01

Il nous faut maintenant transformer ce tableau en format “long” pour les représentations graphiques :

Testo_long <- Testo_large %>% 
  pivot_longer(cols = c(Before, After),
               names_to = "Traitement", 
               values_to = "DO") %>% 
  mutate(Traitement = factor(Traitement, levels = c("Before", "After")))

Testo_long

# A tibble: 26 × 3
   ID    Traitement    DO
   <fct> <fct>      <dbl>
 1 1     Before      4.65
 2 1     After       4.44
 3 2     Before      3.91
 4 2     After       4.3 
 5 3     Before      4.91
 6 3     After       4.98
 7 4     Before      4.5 
 8 4     After       4.45
 9 5     Before      4.8 
10 5     After       5   
# … with 16 more rows

Si vous ne comprenez pas ces commandes, je vous conseille vivement de reprendre les chapitres 5 et 6 du livre en ligne de Biométrie 2. Dans l’idéal, depuis les TP de biométrie 2, vous devriez être capables de construire de telles séquences de commandes pour aboutir à un tableau rangé ne contenant que les variables utiles, au format long comme au format court (ou large). Mais évidemment, de tels groupes de commandes se construisent étape par étape, et pas d’un seul coup, contrairement à ce que les commandes précédentes pourraient laisser croire.

Maintenant que nous disposons de ces 2 tableaux, nous pouvons commencer à décrire nos données.

3.3.1.2 Statistiques descriptives

Pour décrire simplement les données, nous nous en tiendront ici à l’utilisation des fonctions summary() et skim().

Pour la fonction summary(), le plus simple est toujours d’utiliser le tableau au format large :

summary(Testo_large)

       ID        Before          After     
 1      :1   Min.   :3.910   Min.   :4.30  
 2      :1   1st Qu.:4.700   1st Qu.:4.60  
 3      :1   Median :4.800   Median :4.96  
 4      :1   Mean   :4.734   Mean   :4.79  
 5      :1   3rd Qu.:4.880   3rd Qu.:5.00  
 6      :1   Max.   :4.980   Max.   :5.02  
 (Other):7

On constate ici que pour les 2 traitements, les valeurs des différents indices sont très proches entre les 2 séries de données, avec des valeurs de densité optiques (DO) légèrement supérieures après l’opération chirurgicale (sauf pour le premier quartile).

Pour la fonction skim() le plus simple est là aussi d’utiliser le tableau large :

skim(Testo_large)

── Data Summary ────────────────────────
                           Values     
Name                       Testo_large
Number of rows             13         
Number of columns          3          
_______________________               
Column type frequency:                
  factor                   1          
  numeric                  2          
________________________              
Group variables            None       

── Variable type: factor ───────────────────────────────────────────────────────
  skim_variable n_missing complete_rate ordered n_unique top_counts            
1 ID                    0             1 FALSE         13 1: 1, 2: 1, 3: 1, 4: 1

── Variable type: numeric ──────────────────────────────────────────────────────
  skim_variable n_missing complete_rate  mean    sd    p0   p25   p50   p75
1 Before                0             1  4.73 0.280  3.91   4.7  4.8   4.88
2 After                 0             1  4.79 0.262  4.3    4.6  4.96  5   
   p100 hist 
1  4.98 ▁▁▁▃▇
2  5.02 ▂▁▂▁▇

On arrive toutefois aux mêmes résultats avec le tableau long, à condition de grouper les données par traitement (variable Traitement) avec group_by() :

Testo_long %>% 
  group_by(Traitement) %>% 
  skim()

── Data Summary ────────────────────────
                           Values    
Name                       Piped data
Number of rows             26        
Number of columns          3         
_______________________              
Column type frequency:               
  factor                   1         
  numeric                  1         
________________________             
Group variables            Traitement

── Variable type: factor ───────────────────────────────────────────────────────
  skim_variable Traitement n_missing complete_rate ordered n_unique
1 ID            Before             0             1 FALSE         13
2 ID            After              0             1 FALSE         13
  top_counts            
1 1: 1, 2: 1, 3: 1, 4: 1
2 1: 1, 2: 1, 3: 1, 4: 1

── Variable type: numeric ──────────────────────────────────────────────────────
  skim_variable Traitement n_missing complete_rate  mean    sd    p0   p25   p50
1 DO            Before             0             1  4.73 0.280  3.91   4.7  4.8 
2 DO            After              0             1  4.79 0.262  4.3    4.6  4.96
    p75  p100 hist 
1  4.88  4.98 ▁▁▁▃▇
2  5     5.02 ▂▁▂▁▇

3.3.1.3 Exploration graphique

Ici, c’est le tableau rangé au format long qui sera le plus adapté. Lorsque nous avions une unique série de données, nous avons utilisé 3 types de représentations graphiques pour visualiser les données. Nous allons là aussi réaliser ces 3 graphiques. Toutefois, puisque nous avons maintenant plusieurs séries de données, le format des graphiques sera légèrement différent.

Données brutes sous forme de nuage de points (ou de stripchart) :

Testo_long %>% 
  ggplot(aes(x = Traitement, y = DO)) +
  geom_point()

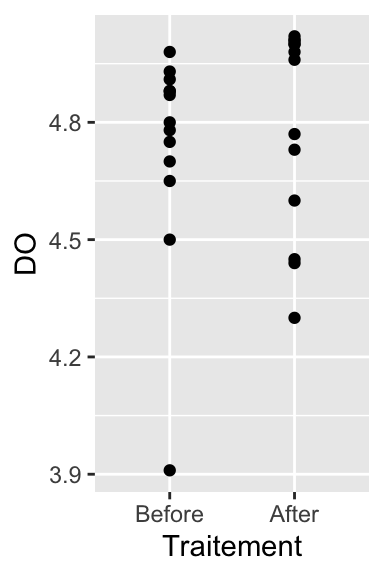
Comme toujours, on peut réaliser un stripchart pour limiter les problèmes d’over-plotting :

Testo_long %>% 
  ggplot(aes(x = Traitement, y = DO)) +
  geom_jitter(height = 0, width = 0.25)

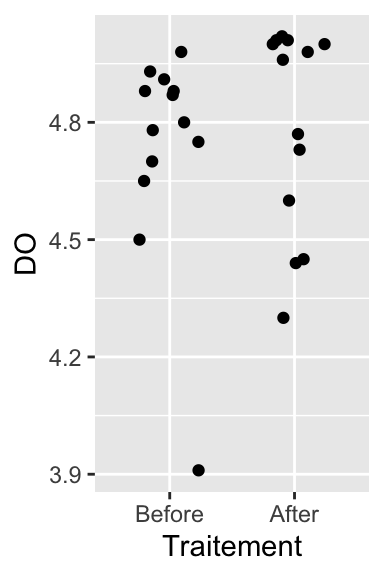
Histogrammes

Nous allons faire un histogramme pour chaque série de données en utilisant des facettes :

Testo_long %>% 
  ggplot(aes(x = DO)) +
  geom_histogram(bins = 10, color = grey(0.8))+
  facet_wrap(~Traitement, ncol = 1)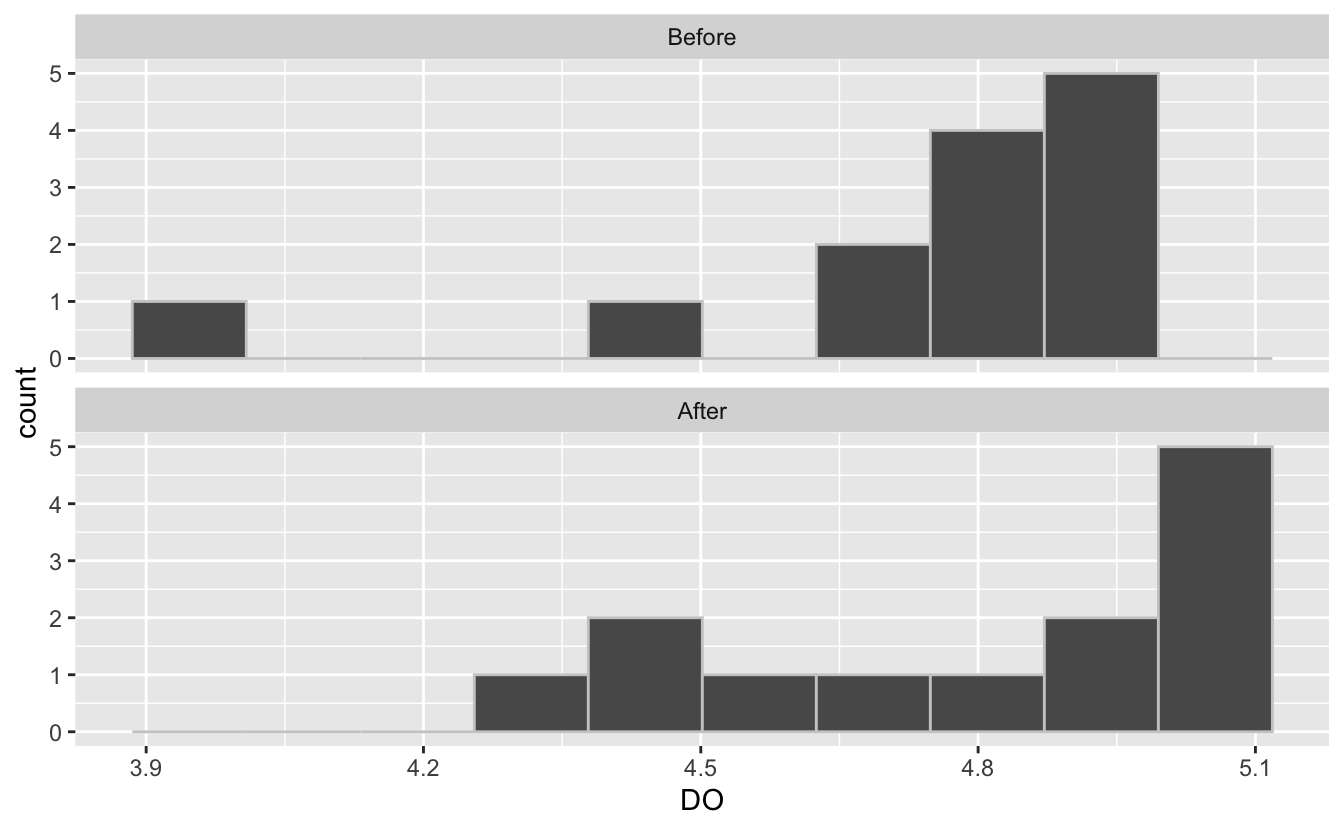

Boxplots

Testo_long %>% 
  ggplot(aes(x = Traitement, y = DO)) +
  geom_boxplot(notch = TRUE)

notch went outside hinges. Try setting notch=FALSE.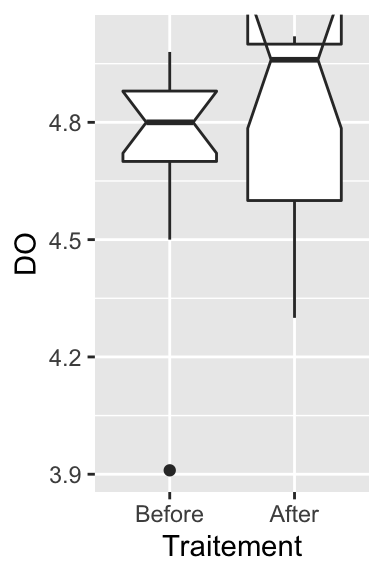

Ici, l’intervalle de confiance à 95% de la médiane pour la série “After” est tellement large que son extrémité supérieure dépasse la valeur du troisième quartile, la valeur maximale observée, et la limite supérieure de l’axe des ordonnées. Il vaut donc mieux ne pas faire figurer les encoches pour avoir un graphique plus présentable :

Testo_long %>% 
  ggplot(aes(x = Traitement, y = DO)) +
  geom_boxplot()

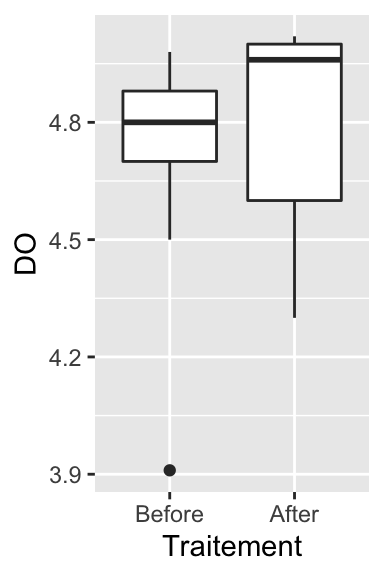
À première vue, ces 3 représentations graphiques semblent montrer que la seconde série de données (après l’opération chirurgicale) présente des valeurs légèrement plus élevées que la première (avant l’opération). Toutefois, il semble que la dispersion des données soit aussi plus importante après l’opération qu’avant, sauf pour un individu outlier qui présente une immuno-compétence très faible avant l’opération.

Toutes ces représentations graphiques sont certes utiles, mais elles masquent un élément crucial : ce sont les mêmes individus qui sont étudiés avant et après l’opération. Il s’agit de données appariées ! Pour avoir une bonne vision de ce qui se passe, il nous faut faire apparaître ce lien entre les 2 séries de données :

Testo_long %>% 
  ggplot(aes(x = Traitement, y = DO, group = ID, color = ID)) +
  geom_line() +
  geom_point(alpha = 0.7)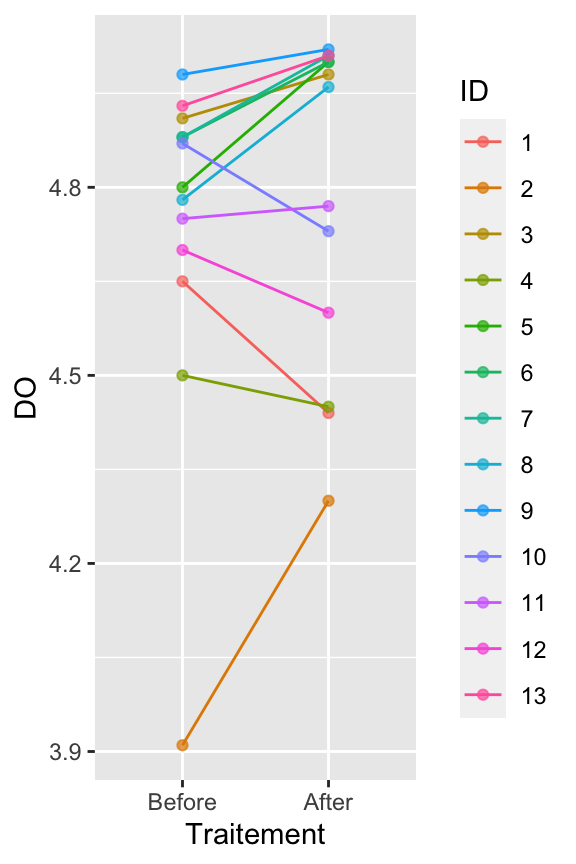

Ce graphique nous donne une image très différente de la réalité des données. On constate ici que l’immuno-compétence de certains individus augmente, alors que pour d’autres, elle diminue.

Une façon d’estimer si les changements d’immuno-compétence sont majoritairement orientés dans un sens ou non est de calculer l’intervalle de confiance à 95% de la différence d’immuno-compétence entre avant et après l’opération.

3.3.2 Le test paramétrique

Le test paramétrique permettant de comparer la moyenne sur des séries appariées est là encore un test de Student : le test de Student sur données appariées (étonnant non ?…). En réalité, ce test de Student n’est pas un test de comparaison de moyennes à proprement parler. La procédure est en fait la suivante :

Pour chaque individu, calculer la différence d’immuno-compétence entre les deux temps de l’expérience (DO après - DO avant)
Puisque nous avons 13 individus, nous aurons 13 valeurs de différences. La moyenne de cette différence sera comparée à la valeur théorique 0. Autrement dit, si les 2 séries ont même moyenne, la moyenne des différences doit être nulle. Sinon, la moyenne des différences doit être différente de zéro.

3.3.2.1 Conditions d’application

Les conditions d’application de ce test paramétrique sont presque les mêmes que pour le test de Student à un échantillon :

Les individus sur lesquels portent la comparaison doivent être issus d’un échantillonnage aléatoire. Comme toujours, en l’absence d’indication contraire, on considère que cette condition est vérifiée.
Les différences par paires entre les 2 modalités du traitement doivent suivre une distribution Normale. Ce n’est donc pas les données brutes de chaque série qui doivent suivre une loi Normale, mais bien la différence “après” - “avant” calculée pour chaque individu. Commençons donc par calculer ces différences :

Testo_large <- Testo_large %>% 
  mutate(Diff = After - Before)

Testo_large

# A tibble: 13 × 4
   ID    Before After    Diff
   <fct>  <dbl> <dbl>   <dbl>
 1 1       4.65  4.44 -0.21  
 2 2       3.91  4.3   0.390 
 3 3       4.91  4.98  0.0700
 4 4       4.5   4.45 -0.0500
 5 5       4.8   5     0.200 
 6 6       4.88  5     0.120 
 7 7       4.88  5.01  0.130 
 8 8       4.78  4.96  0.180 
 9 9       4.98  5.02  0.0400
10 10      4.87  4.73 -0.140 
11 11      4.75  4.77  0.0200
12 12      4.7   4.6  -0.100 
13 13      4.93  5.01  0.0800

Il nous faut donc tester la normalité de la nouvelle variable Diff. Commençons par en faire un graphique :

Testo_large %>% 
  ggplot(aes(x = Diff)) +
  geom_histogram(bins = 10, color = grey(0.8))

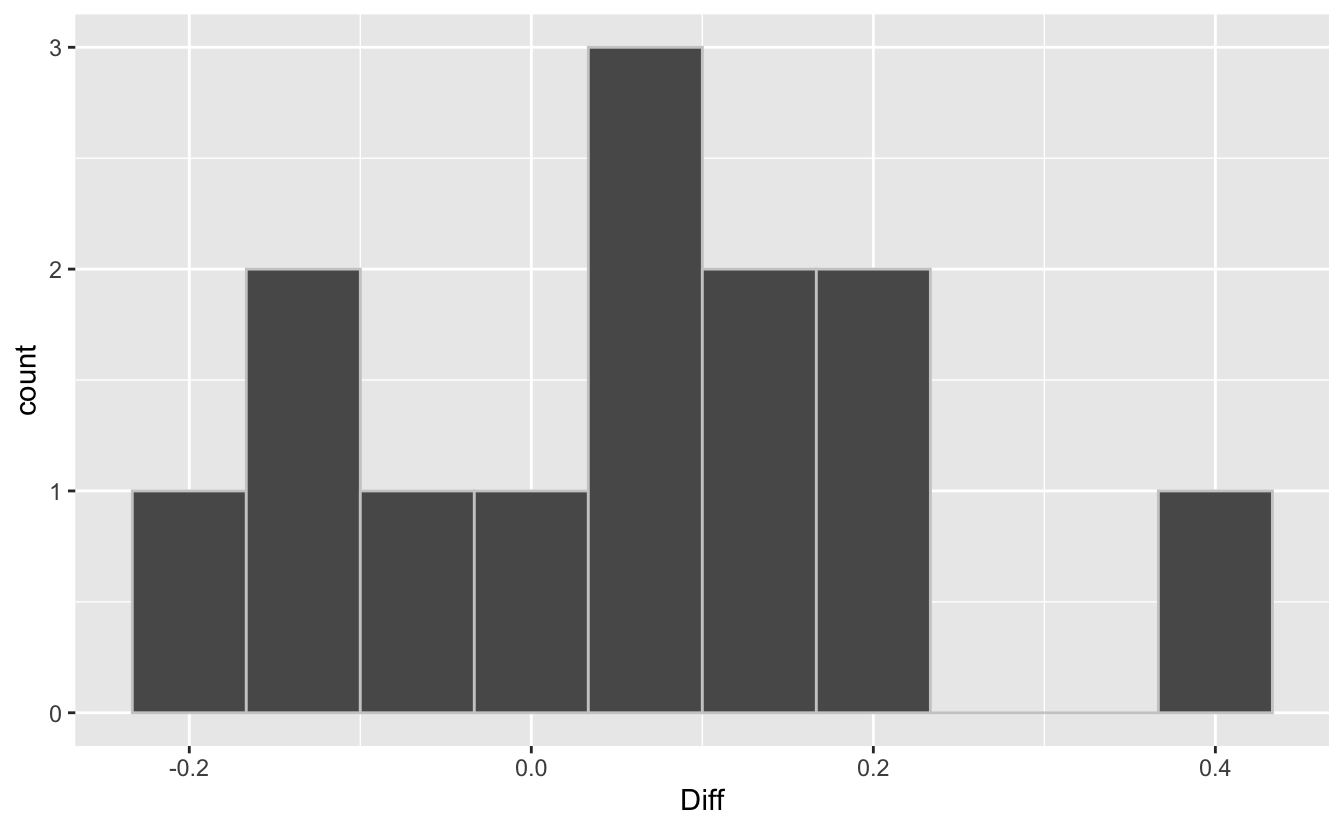
Compte tenu du faible nombre d’individus, la forme de l’histogramme n’est pas si éloignée que ça d’une courbe en cloche (notez que ce n’était pas du tout le cas pour les données brutes de chaque série de départ qui ont toutes les deux des distributions non Normales). On le vérifie avec un test de normalité de Shapiro-Wilk :

H$_0$ : la différence d’immuno-compétence des individus suit une distribution Normale.
H$_1$ : la différence d’immuno-compétence des individus ne suit pas une distribution Normale.

Testo_large %>% 
  pull(Diff) %>% 
  shapiro.test()


    Shapiro-Wilk normality test

data:  .
W = 0.97949, p-value = 0.977

Au seuil $\alpha = 0.05$, on ne peut pas rejeter l’hypothèse nulle de normalité pour la différence d’immuno-compétence entre après et avant l’intervention chirurgicale (test de Shapiro-Wilk, $W = 0.98$, $p = 0.977$).

Les conditions d’application du test paramétrique sont donc réunies.

3.3.2.2 Réalisation du test et interprétation

Le test de Student sur données appariées peut se faire de 3 façons distinctes. Les 3 méthodes fournissent exactement les mêmes résultats. Quelle que soit la méthode utilisée, les hypothèses nulles et alternatives sont toujours les mêmes :

H$_0$ : le changement moyen de production d’anticorps après la pose chirurgicale de l’implant de testostérone est nul ($\mu_{Diff} = 0$).
H$_1$ : le changement moyen de production d’anticorps après la pose chirurgicale de l’implant de testostérone n’est pas nul ($\mu_{Diff} \neq 0$).

# Méthode nº1 : avec une formule et le tableau au format long
t.test(DO ~ Traitement, data = Testo_long, paired = TRUE)


    Paired t-test

data:  DO by Traitement
t = -1.2714, df = 12, p-value = 0.2277
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -0.15238464  0.04007695
sample estimates:
mean of the differences 
            -0.05615385

Plusieurs remarques concernant cette première syntaxe :

On utilise le symbole “~” pour indiquer une formule. On cherche à regarder l’effet du Traitement sur la DO qui traduit l’immuno-compétence. Le “~” se lit : “en fonction de”.
Avec la syntaxe utilisant les formules, on doit spécifier l’argument data = Testo_long pour indiquer à RStudio que les variables DO et Traitement sont des colonnes de ce tableau.
Enfin, il est important d’indiquer paired = TRUE puisque nous réalisons un test de Student sur données appariées. Si on ne mets pas cet argument, on réalise un test de Student sur échantillons indépendants.

Ici, voilà la conclusion de ce test :

Le test de Student sur données appariées ne permet pas de montrer de changement d’immuno-compétence suite à l’intégration de l’implant chirurgical de testostérone. On ne peut pas rejeter l’hypothèse nulle au seuil $\alpha = 0.05$ ($t = -1.27$, $ddl = 12$, $p = 0.223$). La moyenne des différences de densités optiques observées entre avant et après l’intervention chirurgicale vaut -0.056 (intervalle de confiance à 95% de cette différence : [-0.152 ; 0.040])

Donc visiblement, une forte production de testostérone n’est pas significativement associée à une baisse de l’immuno-compétence.

# Méthode nº2 : avec les 2 séries de données et le tableau au format large
t.test(Testo_large$Before, Testo_large$After, paired = TRUE)


    Paired t-test

data:  Testo_large$Before and Testo_large$After
t = -1.2714, df = 12, p-value = 0.2277
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -0.15238464  0.04007695
sample estimates:
mean of the differences 
            -0.05615385

Cette deuxième syntaxe est différente de la première puisque nous n’utilisons plus le format formule. Ici, on indique le nom des 2 colonnes du tableau Testo_large qui contiennent les 2 séries de données. Puisque nous n’utilisons plus de formule, l’argument “data = ...” n’existe plus. C’est pourquoi il nous faut taper spécifiquement “Testo_large$Before” et “Testo_large$After”, et non pas simplement le nom des colonnes. En revanche, comme pour le test précédent, il est indispensable d’indiquer “paired = TRUE” pour faire un test de Student sur données appariées.

Les résultats fournis et leur interprétation sont identiques à ceux de la syntaxe précédente.

# Méthode nº3 : avec la variable Diff, mu = 0, et le tableau au format large
t.test(Testo_large$Diff, mu = 0)


    One Sample t-test

data:  Testo_large$Diff
t = 1.2714, df = 12, p-value = 0.2277
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 -0.04007695  0.15238464
sample estimates:
 mean of x 
0.05615385

Enfin, comme expliqué plus haut, le test de Student sur données appariées est strictement équivalent à un test de Student à un échantillon pour lequel on compare la moyenne des différences individuelles à 0. Là encore, les résultats produits et leur interprétation sont identiques aux deux tests précédents. La seule différence concerne les signes puisque les deux premiers tests regardaient la différence “Before - After” alors que ce troisième test regarde la différence “After - Before” (que nous avons calculée manuellement).

À vous donc de choisir la syntaxe qui vous paraît la plus parlante ou celle que vous avez le plus de facilité à retenir.

3.3.3 L’alternative non paramétrique

Comme pour le test de Student à un échantillon, lorsque les conditions d’application du test de Student sur données appariées ne sont pas vérifiées (c’est à dire lorsque la différence entre les données appariées des deux séries ne suit pas une loi Normale), il faut utiliser un test non paramétrique équivalent.

Il s’agit là encore du test de Wilcoxon des rangs signés qui s’intéresse aux médianes. Les hypothèses nulles et alternatives sont les suivantes :

H$_0$ : le changement médian de production d’anticorps après la pose chirurgicale de l’implant de testostérone est nul ($med_{Diff} = 0$).
H$_1$ : le changement médian de production d’anticorps après la pose chirurgicale de l’implant de testostérone n’est pas nul ($med_{Diff} \neq 0$).

Comme pour le test de Student, 3 syntaxes sont possibles et strictement équivalentes. Il est important de ne pas oublier l’argument paired = TRUE pour les 2 premières syntaxes afin de s’assurer que l’on réalise bien un test sur données appariées. Enfin, l’argument conf.int = TRUE doit être ajouté pour les 3 syntaxes afin que la (pseudo-) médiane et son intervalle de confiance à 95% soient calculés et affichés.

wilcox.test(DO ~ Traitement, data = Testo_long, paired = TRUE, conf.int = TRUE)


    Wilcoxon signed rank exact test

data:  DO by Traitement
V = 30, p-value = 0.3054
alternative hypothesis: true location shift is not equal to 0
95 percent confidence interval:
 -0.145  0.040
sample estimates:
(pseudo)median 
        -0.055

wilcox.test(Testo_large$Before, Testo_large$After, paired = TRUE, 
            conf.int = TRUE)


    Wilcoxon signed rank exact test

data:  Testo_large$Before and Testo_large$After
V = 30, p-value = 0.3054
alternative hypothesis: true location shift is not equal to 0
95 percent confidence interval:
 -0.145  0.040
sample estimates:
(pseudo)median 
        -0.055

wilcox.test(Testo_large$Diff, mu = 0, conf.int = TRUE)


    Wilcoxon signed rank exact test

data:  Testo_large$Diff
V = 61, p-value = 0.3054
alternative hypothesis: true location is not equal to 0
95 percent confidence interval:
 -0.040  0.145
sample estimates:
(pseudo)median 
         0.055

Ici, la conclusion de ce test est :

Le test de Wilcoxon des rangs signés n’a pas permis de montrer de changement d’immuno-compétence suite à l’intégration de l’implant chirurgical de testostérone. On ne peut pas rejeter l’hypothèse nulle au seuil $\alpha = 0.05$ ($V = 61$, $p = 0.305$). La médiane des différences de densités optiques observées entre après et avant l’intervention chirurgicale vaut 0.055 (intervalle de confiance à 95% de cette différence : [-0.040 ; 0.145]).

3.3.4 Exercice d’application

Les autruches vivent dans des environnements chauds et elles sont donc fréquemment exposées au soleil durant de longues périodes. Dans des environnements similaires, les mammifères ont des mécanismes physiologiques leur permettant de réduire la température de leur cerveau par rapport à celle de leur corps. Une équipe de chercheurs (Fuller et al., 2003) a testé si les autruches pouvaient faire de même. La température du corps et du cerveau de 37 autruches a été enregistrée par une journée chaude typique. Les résultats, exprimés en degrés Celsius, figurent dans le fichier Autruches.csv.

Importez ces données et faites-en l’analyse pour savoir s’il existe une différence de température moyenne entre le corps et le cerveau des autruches. Comparez ces résultats avec les prédictions faites pour les mammifères dans un environnement similaire. Comme toujours, vous commencerez par faire une analyse descriptive des données, sous forme numérique et graphique, avant de vous lancer dans les tests d’hypothèses.

3.4 Comparaison de la moyenne de 2 populations : échantillons indépendants

On s’intéresse maintenant aux méthodes permettant de comparer la moyenne de deux groupes ou de deux traitements dans la cas d’échantillons indépendants. Dans ce type de design expérimentaux, les les deux traitements sont appliqués à des échantillons indépendants issus de 2 populations.

3.4.1 Exploration préalable des données

Chez le lézard cornu Phrynosoma mcallii, une frange de piquants entoure la tête. Une équipe d’herpétologues (Young et al., 2004) a étudié la question suivante : des piquants plus longs autour de la tête protègent-ils le lézard cornu de son prédateur naturel, la pie grièche migratrice Lanius ludovicianus ? Ce prédateur a en effet une particularité : il accroche ses proies mortes à des barbelés ou des branches pour les consommer plus tard. Les chercheurs ont donc mesuré la longueur des cornes de 30 lézards retrouvés morts et accrochés dans des arbres par la pie grièche migratrice. Et en parallèle, ils ont mesuré les cornes de 154 individus vivants et en bonne santé choisis au hasard dans la population.

3.4.1.1 Importation et examen visuel

Les données de cette étude sont stockées dans le fichier HornedLizards.csv. Importez ces données dans un objet nommé Lizard et examinez le tableau obtenu.

Lizard

# A tibble: 185 × 2
   squamosalHornLength Survival
                 <dbl> <chr>   
 1                25.2 living  
 2                26.9 living  
 3                26.6 living  
 4                25.6 living  
 5                25.7 living  
 6                25.9 living  
 7                27.3 living  
 8                25.1 living  
 9                30.3 living  
10                25.6 living  
# … with 175 more rows

View(Lizard)

On constate ici 3 choses :

la variable Survival devrait être un facteur.
le nom de la première colonne (squamosalHornLength) est bien trop long
pour un animal vivant, la mesure de longueur des cornes est manquante. Il nous faut donc retirer cet individu.

Nous pouvons facilement réaliser les 3 modifications d’un coup :

Lizard <- Lizard %>% 
  mutate(Survival = factor(Survival)) %>% 
  rename(Horn_len = squamosalHornLength) %>% 
  filter(!is.na(Horn_len))

Lizard

# A tibble: 184 × 2
   Horn_len Survival
      <dbl> <fct>   
 1     25.2 living  
 2     26.9 living  
 3     26.6 living  
 4     25.6 living  
 5     25.7 living  
 6     25.9 living  
 7     27.3 living  
 8     25.1 living  
 9     30.3 living  
10     25.6 living  
# … with 174 more rows

3.4.1.2 Statistiques descriptives

Comme dans la partie précédente sur les données appariées, les statistiques descriptives doivent être réalisées pour chaque groupe d’individus. Ici, le plus simple est d’utiliser la fonction skim() sur les données groupées par niveau du facteur Survival (avec la fonction group_by()) :

Lizard %>% 
  group_by(Survival) %>% 
  skim()

── Data Summary ────────────────────────
                           Values    
Name                       Piped data
Number of rows             184       
Number of columns          2         
_______________________              
Column type frequency:               
  numeric                  1         
________________________             
Group variables            Survival  

── Variable type: numeric ──────────────────────────────────────────────────────
  skim_variable Survival n_missing complete_rate  mean    sd    p0   p25   p50
1 Horn_len      killed           0             1  22.0  2.71  15.2  21.1  22.2
2 Horn_len      living           0             1  24.3  2.63  13.1  23    24.6
    p75  p100 hist 
1  23.8  26.7 ▂▂▇▇▃
2  26    30.3 ▁▁▅▇▂

Outre ces informations sur les ordres de grandeurs observés dans chaque groupe de lézards (vivants ou morts), la fonction skim() ne fournit pas les effectifs observés dans chaque groupe. Pour cela, on peut utiliser une fonction décrite en biométrie 2, la fonction count() :

Lizard %>% 
  count(Survival)

# A tibble: 2 × 2
  Survival     n
  <fct>    <int>
1 killed      30
2 living     154

On constate ici que les tailles d’échantillons sont très différentes. C’est normal compte tenu de la difficulté de repérer des individus morts dans la nature, et ce n’est pas gênant pour nos analyses puisque la taille des deux échantillons reste élevée.

On constate également que si les écarts-types des 2 groupes sont proches, les moyennes et médianes sont plus élevées dans le groupe des individus vivants que dans celui des individus morts (c’est le cas également des quartiles 1 et 3).

3.4.1.3 Exploration graphique

Comme toujours, nous pouvons réaliser 3 types de graphiques pour en apprendre plus sur la distribution des données dans les deux groupes. En revanche, sur le graphique de type “nuage de points”, il est ici impossible de relier les points deux à deux. Non seulement cela n’aurait aucun sens puisque les échantillons sont indépendants, mais en outre, nous ne disposons pas du même nombre d’individus dans les 2 échantillons.

Stripchart

Lizard %>% 
  ggplot(aes(x = Survival, y = Horn_len)) +
  geom_jitter(height = 0, width = 0.2, alpha = 0.5)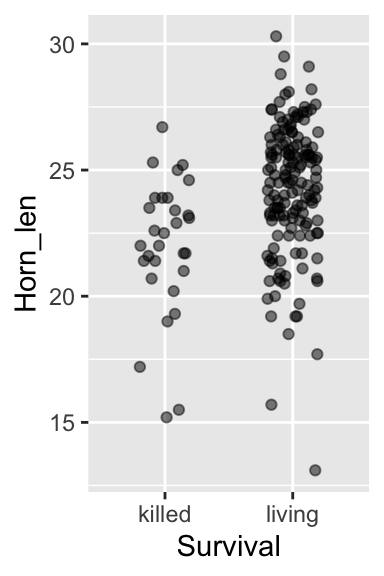

Ce premier graphique permet de visualiser très clairement les différences de tailles d’échantillons entre les deux groupes. Il permet également de voir que l’étendue des longueurs de cornes est plus importante dans le groupe des individus vivants que dans celui des individus morts.

Histogrammes

Lizard %>% 
  ggplot(aes(x = Horn_len)) +
  geom_histogram(bins = 15, color = grey(0.8)) +
  facet_wrap(~Survival, ncol = 1, scales = "free_y")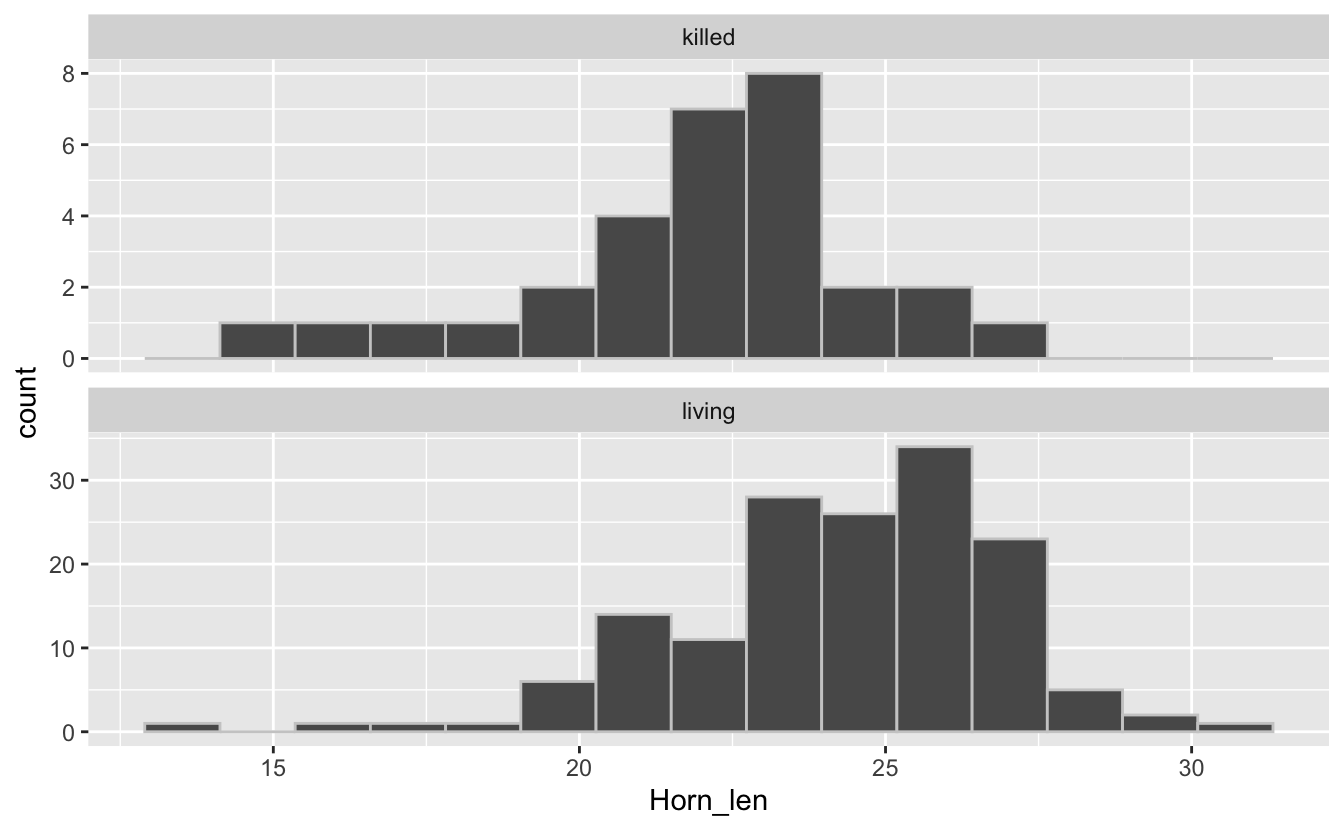

Notez ici l’utilisation de l’argument scales = "free_y" dans la fonction facet_wrap(). Cet argument permet de ne pas imposer la même échelle pour l’axe des ordonnées des 2 graphiques. Ce choix est ici pertinent puisque les effectifs des 2 groupes sont très différents. Faîtes un essai sans cet argument pour voir la différence.

Cette visualisation nous montre que les données doivent suivre à peu près une distribution Normale dans les 2 groupes, et que globalement la longueur des cornes semble légèrement plus élevée dans le groupe des vivants (avec un mode autour de 25-26 mm) que dans le groupes des morts (avec un mode autour de 23-24 mm).

Boxplots

Lizard %>% 
  ggplot(aes(x = Survival, y = Horn_len)) +
  geom_boxplot(notch = TRUE)

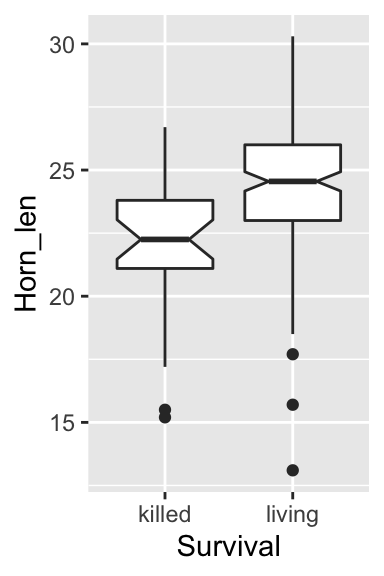
Nous visualisons ici encore plus clairement que sur les histogrammes le fait que les longueurs de cornes des individus vivants sont légèrement plus longues que celles des individus morts. D’ailleurs, puisque les intervalles de confiance à 95% des médianes des 2 groupes (les encoches) ne se chevauchent pas, un test de comparaison des moyennes devrait logiquement conclure à une différence significative en faveur des individus vivants. On peut également noter que la largeur de l’encoche pour les individus morts est plus importante que celle des vivants. Cela traduit une incertitude plus grande autour de la médiane estimée dans le groupe des individus morts. C’est tout à fait logique compte tenu des effectifs modestes dans ce groupe.

3.4.2 Le test paramétrique

Le test paramétrique le plus puissant que nous puissions faire pour comparer la moyenne de 2 populations est le test de Student. Ce test étant paramétrique, nous devons nous assurer que ses conditions d’application sont vérifiées avant de pouvoir le réaliser.

3.4.2.1 Conditions d’application

Les conditions d’application de ce test sont au nombre de 3 :

Chacun des deux échantillons est issu d’un échantillonnage aléatoire de la population générale. Comme toujours, en l’absence d’indication contraire, on considère que cette condition est toujours vérifiée.
La variable numérique étudiée est distribuée normalement dans les deux populations. Il nous faudra donc faire deux test de Shapiro-Wilk, un pour chaque échantillon.
L’écart-type (et la variance) de la variable numérique est la même dans les deux populations. C’est ce que l’on appelle l’homoscédasticité.

En réalité, le test du $t$ de Student sur deux échantillons indépendants est assez robuste face au non respect de cette troisième condition d’application. Cela signifie que si cette troisième condition d’application n’est pas strictement vérifiée, les résultats du tests peuvent malgré tout rester valides. Lorsque les 2 échantillons comparés ont des tailles supérieures ou égales à 30, ce test fonctionne bien même si l’écart-type d’un groupe est jusqu’à 3 fois supérieur ou inférieur à l’écart-type du second groupe, à condition que la taille des 2 échantillons soit proche (ce qui n’est pas le cas ici !). En revanche, si les écart-types diffèrent de plus d’un facteur 3, ou si les tailles d’échantillons sont très différentes, le test du $t$ de Student ne devrait pas être utilisé. De même, si la taille des échantillons est inférieure à 30 et que les variances ne sont pas homogènes, ce test ne devrait pas être réalisé. En conclusion, les résultats du test du $t$ de Student à deux échantillons indépendants peuvent rester valides si la troisième condition d’homoscédasticité est violée, mais dans certains cas seulement.

Le test du $t$ de Student sur deux échantillons indépendants est également assez robuste face à des écarts mineurs à la distribution Normale, tant que la forme des deux distributions comparées reste similaire. En outre, la robustesse de ce test augmente avec la taille des échantillons.

Ici, nous allons donc commencer par vérifier la normalité de chacun des 2 échantillons en réalisant 2 tests de Shapiro-Wilk. Si ces tests confirment que la taille des cornes suit une distribution Normale dans la population générale, nous comparerons alors la variance des 2 populations (nous verrons 3 méthodes pour cela). Les statistiques descriptives réalisées plus haut nous ont montré que les écarts-types des 2 échantillons sont proches, mais que les tailles d’échantillons sont très différentes. L’homoscédasticité doit donc être vérifiée pour que nous ayons le droit de faire le test de Student.

1. Normalité des données

Nous commençons donc par tester la Normalité des 2 populations dont sont issus les échantillons. Pour les individus morts, les hypothèses sont les suivantes :

H$_0$ : la taille des cornes suit une distribution Normale dans la population des lézards cornus morts.
H$_1$ : la taille des cornes ne suit pas une distribution Normale dans la population des lézards cornus morts.

Lizard %>% 
  filter(Survival == "killed") %>% 
  pull(Horn_len) %>% 
  shapiro.test()


    Shapiro-Wilk normality test

data:  .
W = 0.93452, p-value = 0.06482

La $p$-value est supérieure à $\alpha = 0.05$, donc on ne peut pas rejeter l’hypothèse nulle de normalité pour la taille des cornes de la population des lézards cornus morts (test de Shapiro-Wilk, $W = 0.93$, $p = 0.065$).

Pour les individus vivants :

H$_0$ : la taille des cornes suit une distribution Normale dans la population des lézards cornus vivants.
H$_1$ : la taille des cornes ne suit pas une distribution Normale dans la population des lézards cornus vivants.

Lizard %>% 
  filter(Survival == "living") %>% 
  pull(Horn_len) %>% 
  shapiro.test()


    Shapiro-Wilk normality test

data:  .
W = 0.96055, p-value = 0.0002234

La $p$-value est inférieure à $\alpha = 0.05$, donc on rejette l’hypothèse nulle de normalité pour la taille des cornes de la population des lézards cornus vivants (test de Shapiro-Wilk, $W = 0.96$, $p < 0.001$).

Si l’on examine l’histogramme des 2 échantillons, on constate toutefois que la forme des distributions des 2 séries de données est très proche. Pour les 2 échantillons, la distribution est en effet uni-modale, avec une asymétrie gauche assez marquée (une longue queue de distribution du côté gauche). La forme des distributions étant similaire (on parle bien de la forme des histogrammes et non de la position du pic), et les histogrammes étant proches de la forme typique d’une courbe en cloche, le test de Student devrait rester valide. En toute rigueur, il faudrait cependant préférer son alternative non paramétrique.

2. Homogénéité des variances

Le test le plus simple pour comparer la variance de 2 populations est le test $F$ :

H$_0$ : la variance des 2 populations est égale, leur ratio vaut 1 $\left(\frac{\sigma^2_{killed}}{\sigma^2_{living}} = 1\right)$.
H$_1$ : la variance des 2 populations est différente, leur ratio ne vaut pas 1 $\left(\frac{\sigma^2_{killed}}{\sigma^2_{living}} \neq 1\right)$.

var.test(Horn_len ~ Survival, data = Lizard)


    F test to compare two variances

data:  Horn_len by Survival
F = 1.0607, num df = 29, denom df = 153, p-value = 0.7859
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.6339331 1.9831398
sample estimates:
ratio of variances 
          1.060711

Ici, le ratio des variances (la variance des individus morts divisée par la variance des individus vivants) est très proche de 1 ($F = 1.06$, IC 95% : [0.63 ; 1.98]). Le test $F$ nous montre qu’il est impossible de rejeter H$_0$ : au seuil $\alpha = 0.05$, le ratio des variances n’est pas significativement différent de 1 (ddl = 29 et 153, $p = 0.79$), les variances sont homogènes.

Le test de Bartlett est un autre test qui permet de comparer la variance de plusieurs populations (2 ou plus). Lorsque le nombre de populations est égal à 2 (comme ici), ce test est absolument équivalent au test $F$ ci-dessus.

H$_0$ : toutes les populations ont même variance ($\sigma^2_A = \sigma^2_B = \sigma^2_C = \cdots = \sigma^2_N$).
H$_1$ : au moins une population a une variance différente des autres.

bartlett.test(Horn_len ~ Survival, data = Lizard)


    Bartlett test of homogeneity of variances

data:  Horn_len by Survival
Bartlett's K-squared = 0.042411, df = 1, p-value = 0.8368

Enfin, le test de Levene devrait être préféré la plupart du temps. Comme le test de Bartlett, il permet de comparer la variance de plusieurs populations, mais il est plus robuste vis à vis de la non-normalité des données.

H$_0$ : toutes les populations ont même variance ($\sigma^2_A = \sigma^2_B = \sigma^2_C = \cdots = \sigma^2_N$).
H$_1$ : au moins une population a une variance différente des autres.

# Le test de Levene fait partie du package car. Il doit être chargé en mémoire
# library(car)
leveneTest(Horn_len ~ Survival, data = Lizard)

Levene's Test for Homogeneity of Variance (center = median)
       Df F value Pr(>F)
group   1  0.0035  0.953
      182

Ici encore, les conclusions sont les mêmes :

Il est impossible de rejeter l’hypothèse nulle d’homogénéité des variances au seuil $\alpha = 0.05$ (test de Levene, $F$ = 0.004, ddl = 1, $p = 0.953$).

3.4.2.2 Réalisation du test et interprétation

Puisque la taille des cornes du lézard cornu suit approximativement la même distribution “presque Normale” dans les 2 populations (lézards morts et vivants) et que ces 2 populations ont des variances homogènes, on peut réaliser le test du $t$ de Student sur deux échantillons indépendants.

H$_0$ : la moyenne des 2 populations est égale, leur différence vaut 0 ($\mu_{killed}-\mu_{living} = 0$).
H$_1$ : la moyenne des 2 populations est différente, leur différence ne vaut pas 0 ($\mu_{killed}-\mu_{living} \neq 0$).

t.test(Horn_len ~ Survival, data = Lizard, var.equal = TRUE)


    Two Sample t-test

data:  Horn_len by Survival
t = -4.3494, df = 182, p-value = 2.27e-05
alternative hypothesis: true difference in means between group killed and group living is not equal to 0
95 percent confidence interval:
 -3.335402 -1.253602
sample estimates:
mean in group killed mean in group living 
            21.98667             24.28117

Notez bien la syntaxe :

Nous utilisons ici la syntaxe du type “formule” faisant appel au symbole “~” (Longueur des cornes en fonction de la Survie) et à l’argument “data =”.
L’argument “paired = TRUE” a disparu puisque nous avons ici deux échantillons indépendants
L’argument “var.equal = TRUE” doit obligatoirement être spécifié : nous nous sommes assuré que l’homogénéité des variances était vérifiée. Il faut donc l’indiquer à R afin que le test de Student classique soit réalisé. Si on omet de le spécifier, c’est un autre test qui est réalisé (voir plus bas).

Au seuil $\alpha$ de 5%, on rejette l’hypothèse nulle d’égalité des moyennes de la longueur des cornes entre lézards vivants et morts (test $t$ de Student sur deux échantillons indépendant, $t = -4.35$, ddl = 182, $p < 0.001$). Les lézards morts ont en moyenne des cornes plus courtes ($\hat{\mu}_{killed} = 21.99$ millimètres) que les lézards vivants ($\hat{\mu}_{living} = 24.28$ millimètres). La gamme des valeurs les plus probables pour la différence de moyenne entre les deux populations est fournie par l’intervalle de confiance à 95% de la différence de moyennes : [-3.34 ; -1.25].

Ce test confirme donc bien l’impression des chercheurs : les lézards principalement pris pour cibles par les pies grièches migratrices ont des cornes en moyenne plus courtes (probablement entre 1.25 et 3.34 millimètres de moins) que les lézards de la population générale. Avoir des cornes plus longues semble donc protéger les lézards de la prédation, du moins dans une certaine mesure.

3.4.3 L’alternative non paramétrique

Si les conditions d’application du test de Student ne sont pas vérifiées, nous devons utiliser un équivalent non paramétrique. C’est le cas du test de Wilcoxon sur la somme des rangs (également appelé test de Mann-Whitney). Comme pour tous les tests de Wilcoxon, la comparaison porte alors non plus sur les moyennes mais sur les médianes.

H$_0$ : la médiane des 2 populations est égale, leur différence vaut 0 ($med_{killed}-med_{living} = 0$).
H$_1$ : la médiane des 2 populations est différente, leur différence ne vaut pas 0 ($med_{killed}-med_{living}\neq 0$).

wilcox.test(Horn_len ~ Survival, data = Lizard, conf.int = TRUE)


    Wilcoxon rank sum test with continuity correction

data:  Horn_len by Survival
W = 1181.5, p-value = 2.366e-05
alternative hypothesis: true location shift is not equal to 0
95 percent confidence interval:
 -3.200076 -1.300067
sample estimates:
difference in location 
             -2.200031

L’argument var.equal = TRUE n’existe pas pour ce test, puisque c’est justement un test non paramétrique qui ne requiert pas l’homogénéité des variances. En revanche, comme pour tous les autres tests de Wilcoxon que nous avons réalisés dans ce TP, l’argument conf.int = TRUE permet d’afficher les estimateurs pertinents, ici, la différence de médiane entre les 2 populations et l’intervalle de confiance à 95% de cette différence de médiane.

La conclusion est ici la même que pour le test de Student : puisque la $p$-value est très inférieure à $\alpha$, on rejette l’hypothèse nulle : les médianes sont bel et bien différentes.

Enfin, dans le cas où la variable étudiée suit la loi Normale dans les deux populations mais qu’elle n’a pas la même variance dans les deux populations, il est toujours possible de réaliser un test de Wilcoxon, mais il est souvent préférable de réaliser un test de Student modifié : le test approché du $t$ de Welch. Ce test est moins puissant que le test de Student classique, mais il reste plus puissant que le test de Wilcoxon, et surtout, il permet de comparer les moyennes et non les médianes

H$_0$ : la moyenne des 2 populations est égale, leur différence vaut 0 ($\mu_{killed}-\mu_{living} = 0$).
H$_1$ : la moyenne des 2 populations est différente, leur différence ne vaut pas 0 ($\mu_{killed}-\mu_{living} \neq 0$).

t.test(Horn_len ~ Survival, data = Lizard)


    Welch Two Sample t-test

data:  Horn_len by Survival
t = -4.2634, df = 40.372, p-value = 0.0001178
alternative hypothesis: true difference in means between group killed and group living is not equal to 0
95 percent confidence interval:
 -3.381912 -1.207092
sample estimates:
mean in group killed mean in group living 
            21.98667             24.28117

La seule différence par rapport à la syntaxe du test $t$ de Student paramétrique est la suppression de l’argument var.equal = TRUE. Attention donc, à bien utiliser la syntaxe correcte. Le test du $t$ de Welch ne devrait être réalisé que lorsque la normalité est vérifiée pour les 2 populations, mais pas l’homoscédasticité. Par rapport au test de Student classique, on constate que le nombre de degrés de libertés est très différent, et donc la $p$-value également. Les bornes de l’intervalle de confiance à 95% de la différence de moyenne sont différentes également puisque leur calcul a été fait en supposant que les 2 populations n’avaient pas même variance.

3.4.4 Exercice d’application

On s’intéresse à la différence de taille supposée entre hommes et femmes. Le fichier HommesFemmes.xls contient les tailles en centimètres de 38 hommes et 43 femmes choisis au hasard parmi les étudiants de première année à La Rochelle Université. Importez, mettez en forme et analysez ces données. Vous prendrez soin de retirer les éventuelles valeurs manquantes, vous prendrez le temps d’examiner les données à l’aide de statistiques descriptives et de représentations graphiques adaptées, puis vous tenterez de répondre à la question suivante : les hommes et les femmes inscrits en première année à La Rochelle Université ont-il la même taille ? Si non, caractérisez cette différence de taille.

3.5 Tests bilatéraux et unilatéraux

3.5.1 Principe

Jusqu’à maintenant, tous les tests que nous avons réalisés sont des tests bitaléraux. Pour chaque test, l’hypothèse nulle est imposée. En revanche, pour certains tests, l’hypothèse alternative est à choisir (et à spécifier) par l’utilisateur parmi 3 possibilités :

Une hypothèse bilatérale. C’est celle qui est utilisée par défaut si l’utilisateur ne précise rien.
Deux hypothèses unilatérales possibles, qui doivent être spécifiées explicitement par l’utilisateur.

Les tests unilatéraux peuvent concerner tous les tests pour lesquels les hypothèses sont de la forme suivante :

H$_0$ : la valeur d’un paramètre de la population est égale à $k$ ($k$ peut être une valeur fixe, arbitraire, choisie par l’utilisateur, ou la valeur d’un paramètre d’une autre populations).
H$_1$ : la valeur d’un paramètre de la population n’est pas égale à $k$.

En réalité, si nous remplaçons l’hypothèse H$_1$ par :

H$_1$ : la valeur d’un paramètre de la population est supérieure à $k$.

ou par :

H$_1$ : la valeur d’un paramètre de la population est inférieure à $k$.

nous réalisons un test unilatéral.

Dans R, la syntaxe permettant de spécifier l’hypothèse alternative que nous souhaitons utiliser est toujours la même. Il faut préciser, au moment de faire le test l’argument suivant :

alternative = "two.sided" : pour faire un test bilatéral. Si on ne le fait pas explicitement, c’est de toutes façons cette valeur qui est utilisée par défaut.
alternative = "greater" : pour choisir l’hypothèse unilatérale “>”.
alternative = "less" : pour choisir l’hypothèse unilatérale “<”.

Attention : le choix d’utiliser “greater” ou “less” dépend donc de l’ordre dans lequel les échantillons sont spécifiés. Cette synatxe est valable pour tous les tests de Student vus jusqu’ici (un échantillon, deux échantillons appariés, deux échantillons indépendants) et pour leurs alternatives non paramétriques (test de Wilcoxon des rangs signés, test de Wilcoxon de la somme des rangs, test du $t$ de Welch).

Attention : comme indiqué en TD, l’utilisation de tests unilatéraux doit être réservée exclusivement aux situations pour lesquelles le choix de l’hypothèse unilatérale est possible à justifier par un mécanisme quelconque (biologique, physiologique, comportemental, écologique, génétique, évolutif, biochimique, etc.). Observer que l’un des échantillons a une moyenne plus grande ou plus faible qu’un autre lors de la phase des statistiques descriptives des données n’est pas du tout une raison suffisante. Il faut pouvoir justifier le choix de l’hypothèse alternative par une explication valable. Lorsqu’il est pertinent de réaliser un test unilatéral, on doit toujours le faire, car toutes choses étant égales par ailleurs, un test unilatéral est toujours plus puissant qu’un test bilatéral. Reprenons l’un des exemples examinés précédemment pour mieux comprendre comment tout cela fonctionne.

3.5.2 Un exemple pas à pas

Reprenons l’exemple des lézards cornus. L’étude a été réalisée parce que les chercheurs supposaient que la longueur des cornes des lézards était susceptible de leur fournir une protection face à la prédation. Autrement dit, les chercheurs supposaient que des cornes plus longues devaient fournir une meilleure protection vis à vis de la prédation. Ainsi, les lézards morts devaient avoir des cornes moins longues en moyenne que les les lézards vivants, simplement parce que porter des cornes courtes expose plus fortement les individus à la prédation. Nous avons donc une bonne raison “écologique/évolutive” de considérer un test unilatéral (la susceptibilité face à la prédation qui a entraîné une pression de sélection sur la longueur des cornes des lézards).

Lorsque nous avons examiné cette question, nous avons fait le test du $t$ de Student sur échantillons indépendants de la façon suivante :

t.test(Horn_len ~ Survival, data = Lizard, var.equal = TRUE)


    Two Sample t-test

data:  Horn_len by Survival
t = -4.3494, df = 182, p-value = 2.27e-05
alternative hypothesis: true difference in means between group killed and group living is not equal to 0
95 percent confidence interval:
 -3.335402 -1.253602
sample estimates:
mean in group killed mean in group living 
            21.98667             24.28117

Comme l’indiquent les résultats fournis, l’hypothèse alternative utilisée pour faire le test est : “La vraie différence de moyenne n’est pas égale à 0”. Autrement dit, nous avons fait un test bilatéral avec les hypothèses suivantes :

H$_0$ : la moyenne des 2 populations est égale, leur différence vaut 0 ($\mu_{killed}-\mu_{living} = 0$).
H$_1$ : la moyenne des 2 populations est différente, leur différence ne vaut pas 0 ($\mu_{killed}-\mu_{living} \neq 0$).

Ce test est donc rigoureusement équivalent à celui-ci :

t.test(Horn_len ~ Survival, 
       data = Lizard, var.equal = TRUE,
       alternative = "two.sided")


    Two Sample t-test

data:  Horn_len by Survival
t = -4.3494, df = 182, p-value = 2.27e-05
alternative hypothesis: true difference in means between group killed and group living is not equal to 0
95 percent confidence interval:
 -3.335402 -1.253602
sample estimates:
mean in group killed mean in group living 
            21.98667             24.28117

Ici, nous souhaitons en fait réaliser un test unilatéral avec les hypothèses suivantes :

H$_0$ : la moyenne de longueur des cornes de la population des lézards morts est égale à celle des lézards vivants. Leur différence vaut 0 ($\mu_{killed}-\mu_{living} = 0$).
H$_1$ : la moyenne de longueur des cornes de la population des lézards morts est inférieure à celle des lézards vivants. Leur différence est inférieure à 0 ($\mu_{killed}-\mu_{living} < 0$).

t.test(Horn_len ~ Survival, 
       data = Lizard, var.equal = TRUE,
       alternative = "less")


    Two Sample t-test

data:  Horn_len by Survival
t = -4.3494, df = 182, p-value = 1.135e-05
alternative hypothesis: true difference in means between group killed and group living is less than 0
95 percent confidence interval:
      -Inf -1.422321
sample estimates:
mean in group killed mean in group living 
            21.98667             24.28117

Puisque la $p$-value de ce test est inferieure à $\alpha = 0.05$, on rejette l’hypothèse nulle de l’égalité des moyennes. On valide donc l’hypothèse alternative : les lézards cornus morts ont en moyenne des cornes plus courtes que les lézards vivants. Cette différence de longueur de cornes est en faveur des lézards vivants et vaut très probablement au moins $1.4$ millimètres (c’est l’intervalle de confiance à 95% de la différence de moyennes qui nous le dit).

Dernière chose importante : il ne faut pas se tromper dans le choix de l’hypothèse alternative. En effet, nous aurions pu tenter de tester exactement la même chose en formulant les hypothèses suivantes :

H$_0$ : la moyenne de longueur des cornes de la population des lézards vivants est égale à celle des lézards morts. Leur différence vaut 0 ($\mu_{living}-\mu_{killed} = 0$).
H$_1$ : la moyenne de longueur des cornes de la population des lézards vivants est supérieure à celle des lézards morts. Leur différence est supérieure à 0 ($\mu_{living}-\mu_{killed} > 0$).

Ce test est normalement exactement le même que précédemment. Toutefois, si on essaie de le réaliser, on rencontre un problème :

t.test(Horn_len ~ Survival, 
       data = Lizard, var.equal = TRUE,
       alternative = "greater")


    Two Sample t-test

data:  Horn_len by Survival
t = -4.3494, df = 182, p-value = 1
alternative hypothesis: true difference in means between group killed and group living is greater than 0
95 percent confidence interval:
 -3.166684       Inf
sample estimates:
mean in group killed mean in group living 
            21.98667             24.28117

Ici, la $p$-value est très supérieure à $\alpha$ puisqu’elle vaut 1. Une $p$-value de 1 devrait toujours attirer votre attention. La conclusion devrait donc être que l’on ne peut pas rejeter H$_0$ : les lézards morts et vivants ont en moyenne des cornes de même longueur. Nous savons pourtant que c’est faux.

Le problème est ici liè à l’ordre des catégories “vivant” ou “mort” dans le facteur Survival du tableau Lizard. Les dernières lignes des tests que nous venons de faire indiquent la moyenne de chaque groupe, mais le groupe “killed” apparaît toujours avant le groupe “living”. C’est l’ordre des niveaux dans le facteur Survival qui doit dicter la syntaxe appropriée :

Lizard$Survival

  [1] living living living living living living living living living living
 [11] living living living living living living living living living living
 [21] living living living living living living living living living living
 [31] living living living living living living living living living living
 [41] living living living living living living living living living living
 [51] living living living living living living living living living living
 [61] living living living living living living living living living living
 [71] living living living living living living living living living living
 [81] living living living living living living living living living living
 [91] living living living living living living living living living living
[101] living living living living living living living living living living
[111] living living living living living living living living living living
[121] living living living living living living living living living living
[131] living living living living living living living living living living
[141] living living living living living living living living living living
[151] living living living living killed killed killed killed killed killed
[161] killed killed killed killed killed killed killed killed killed killed
[171] killed killed killed killed killed killed killed killed killed killed
[181] killed killed killed killed
Levels: killed living

Par défaut, dans R, les niveaux d’un facteur sont classés par ordre alphabétique sauf si on spécifie manuellement un ordre différent. Ici, le niveau “killed” est donc le premier niveau du facteur, et “living” le second. Lorsque l’on réalise un test de Student avec ces données (ou un test de Wilcoxon d’ailleurs), la différence de moyenne qui est examinée par le test est donc “moyenne des killed - moyenne des living”. Lorsque nous avons tapé ceci :

t.test(Horn_len ~ Survival, 
       data = Lizard, var.equal = TRUE,
       alternative = "greater")

nous avons en réalité posé les hypothèses suivantes :

H$_0$ : la moyenne de longueur des cornes de la population des lézards morts est égale à celle des lézards vivants. Leur différence vaut 0 ($\mu_{killed}-\mu_{living} = 0$).
H$_1$ : la moyenne de longueur des cornes de la population des lézards morts est supérieure à celle des lézards vivants. Leur différence est supérieure à 0 ($\mu_{killed}-\mu_{living} > 0$).

Ce test est donc erronné, ce qui explique qu’il nous renvoie un résultat faux et une $p$-value de 1. Ici, puisque l’ordre des catégories est “killed” d’abord et “living” ensuite, la seule façon correcte de faire un test unilatéral qui a du sens est donc celle que nous avons réalisée en premier :

t.test(Horn_len ~ Survival, 
       data = Lizard, var.equal = TRUE,
       alternative = "less")

3.5.3 Exercice d’application

Reprenez chaque exemple et exercice de cette séance de TP et identifiez les situations où un test unilatéral aurait du sens. Si vous en trouvez, faites ce test et assurez-vous que les hypothèses choisies sont bien celles qui sont utilisées lors du test.

References

Fox J, Weisberg S, & Price B. (2021). Car: Companion to applied regression. Retrieved from https://CRAN.R-project.org/package=car

Fuller A, Kamerman PR, Maloney SK, Mitchell G, & Mitchell D. (2003). Variability in brain and arterial blood temperatures in free-ranging ostriches in their natural habitat. Journal of Experimental Biology, 206(7), 1171–1181. https://doi.org/10.1242/jeb.00230

Hasselquist D, Marsh JA, Sherman PW, & Wingfield JC. (1999). Is avian humoral immunocompetence suppressed by testosterone? Behavioral Ecology and Sociobiology, 45(3), 167–175. https://doi.org/10.1007/s002650050550

Waring E, Quinn M, McNamara A, Arino de la Rubia E, Zhu H, & Ellis S. (2021). Skimr: Compact and flexible summaries of data. Retrieved from https://CRAN.R-project.org/package=skimr

Wickham H. (2021). Tidyverse: Easily install and load the tidyverse. Retrieved from https://CRAN.R-project.org/package=tidyverse

Wickham H, & Bryan J. (2022). Readxl: Read excel files. Retrieved from https://CRAN.R-project.org/package=readxl

Wickham H, Hester J, & Bryan J. (2022). Readr: Read rectangular text data. Retrieved from https://CRAN.R-project.org/package=readr

Young KV, Brodie ED, & Brodie ED. (2004). How the horned lizard got its horns. Science, 304(5667), 65–65. https://doi.org/10.1126/science.1094790